Blender宝典01-02,改线
精华07/10215 浏览综合
我觉得工作喝咖啡怪怪的,我的意思是:你确定要拿着自己的钱买咖啡然后给老板创造收益的同时还要安慰自己是高级打工人吗…
驴拉磨累了也不会给自己两鞭子啊…

在上一节课中,我们学习了基本的内容,今天我们要学习如何改线,这将会是未来所有建模的基础,也因为如此,实操的难度会非常高,或者说,本宝典的所有内容都是高难度内容,因为在未来,你一定会碰到属于你的逆天模型
本节课你要学到的内容:
融并式曲线切边路径
旋转边式曲线切边路径和其他应用(保护术,开门术)
倒角式曲线切边路径
融并式曲线切边路径
当你学完了基础的竖向和横向的操作时,我们必须了解一个非常常见的情况,那就是创建曲线切边路径,我不知道这个技术其他人是怎么称呼的,但在这里,我就以曲线切边路径为名
在上一节课,我教会了大家如何创建” 网格边缘切线走向”,这种技术是一种让路径拐弯的技术
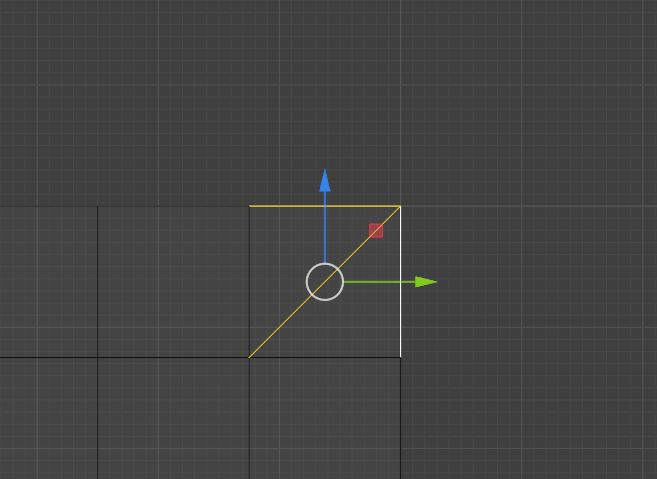
我们接下来的问题是:假如我们的路径不在网格边缘,而在于内部的切线呢?
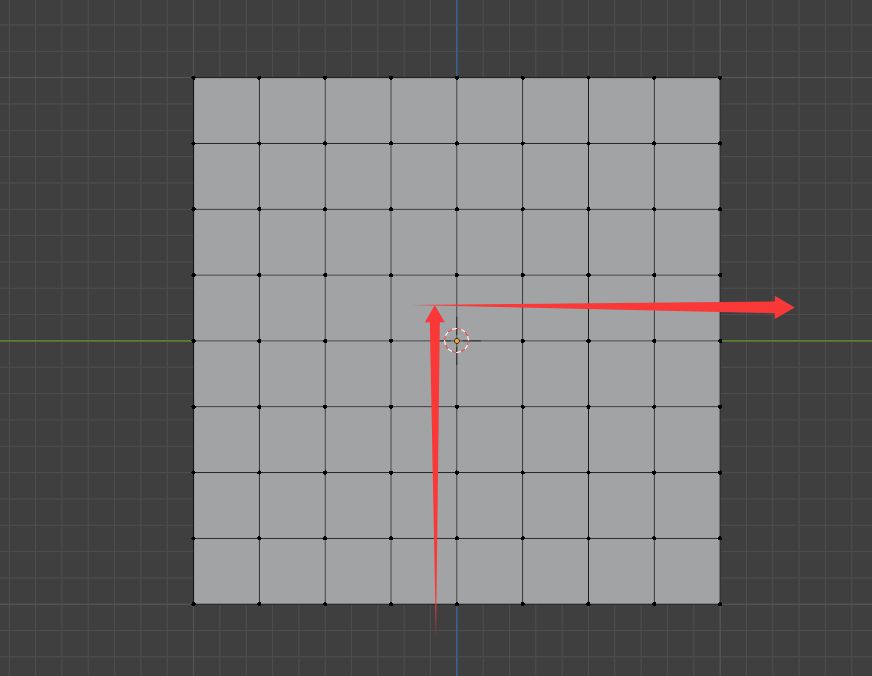
在上一节课中,我有说过,不管一个四边面形变成任何形状,它都有一个对角边给我们提供切线操作
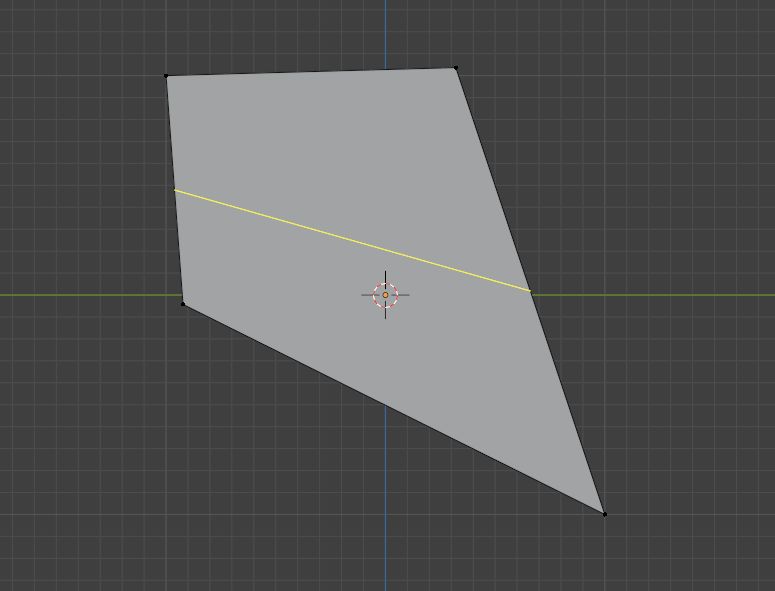
基于这个特性:我们可以拿出一个基础的长方体
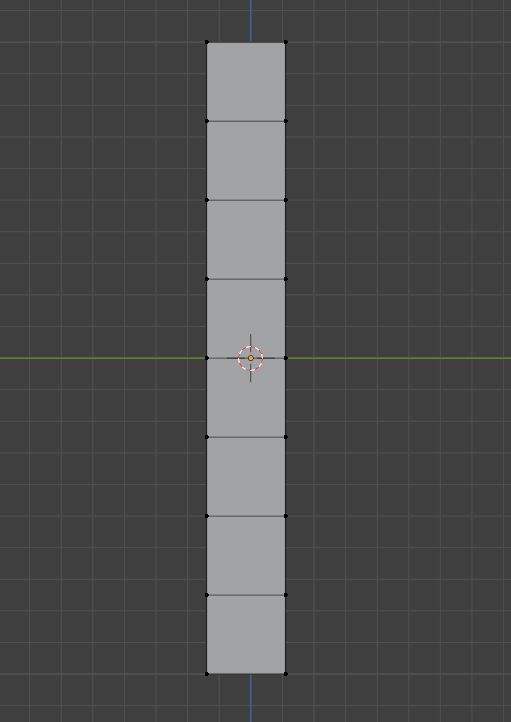
然后将转折的点往下拉
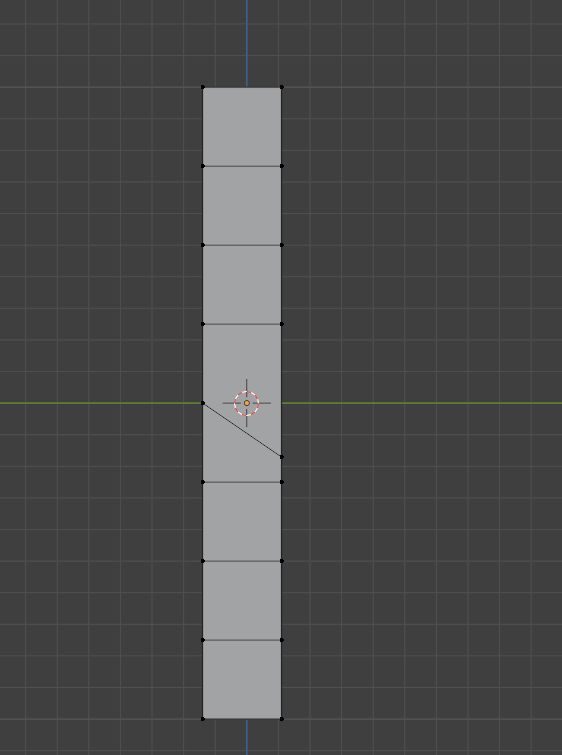
然后将上面的边旋转90度就可以了
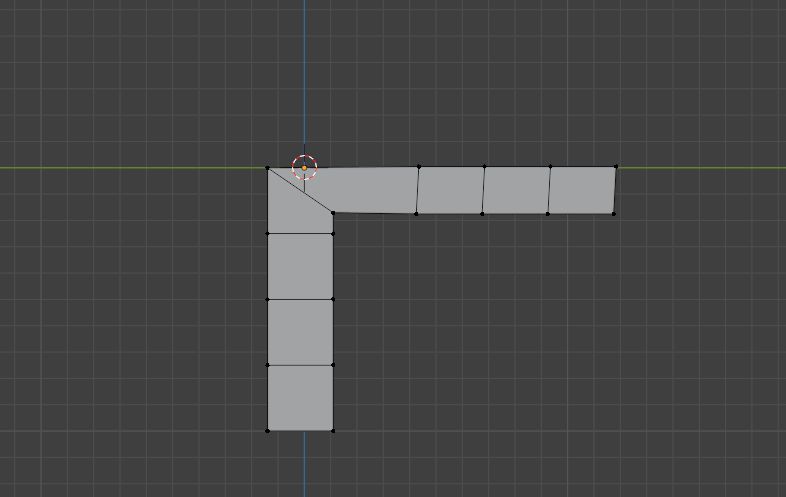
基于这个技术,我们可以先拿出一个拐弯的长方体
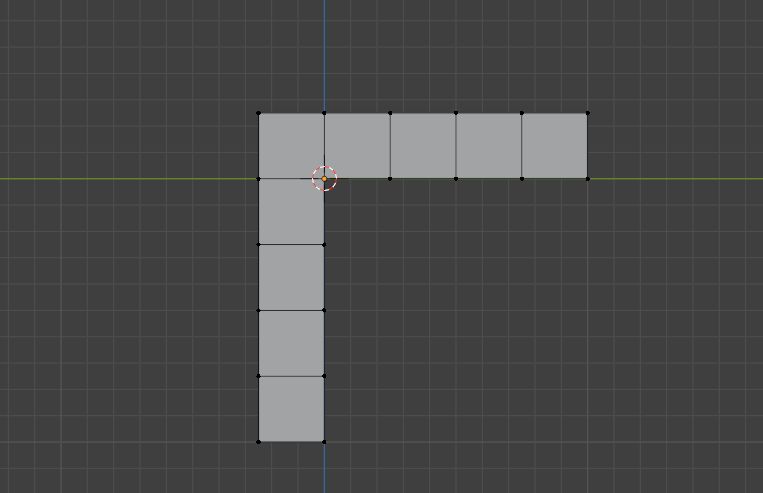
然后把点合并到左上角的点
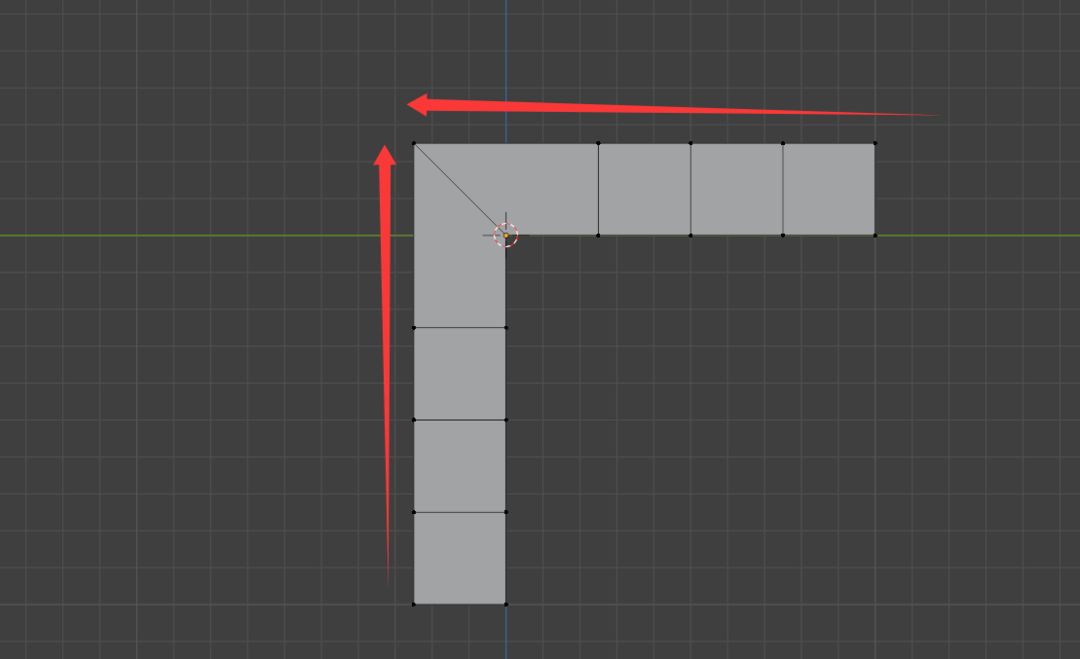
此时我们就会发现切线拐弯了
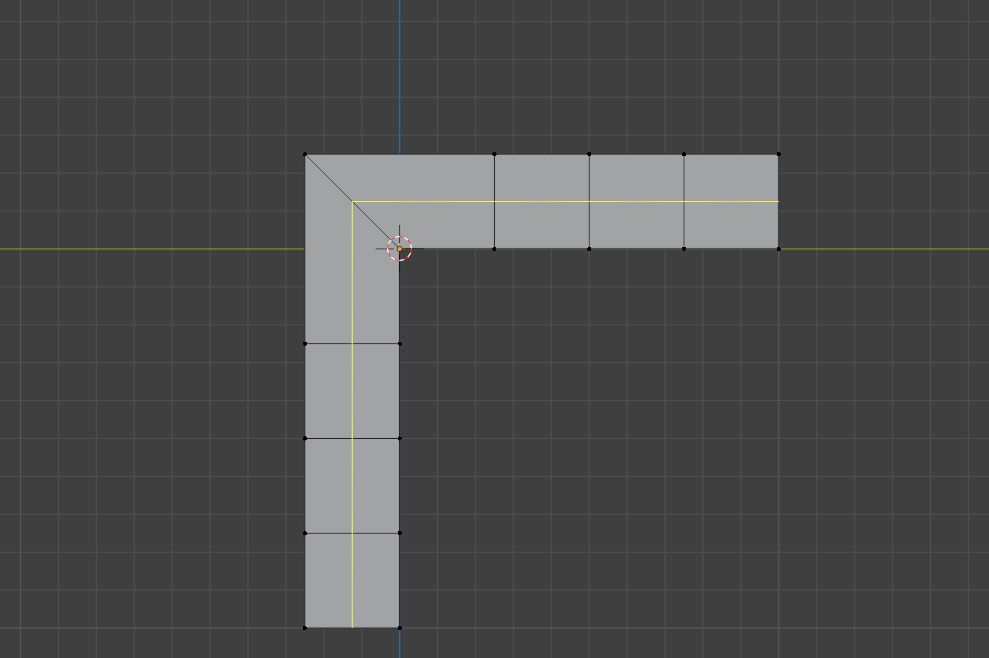
那么回到之前的平面上:想要让布线拐弯,我们只需要重复以上操作
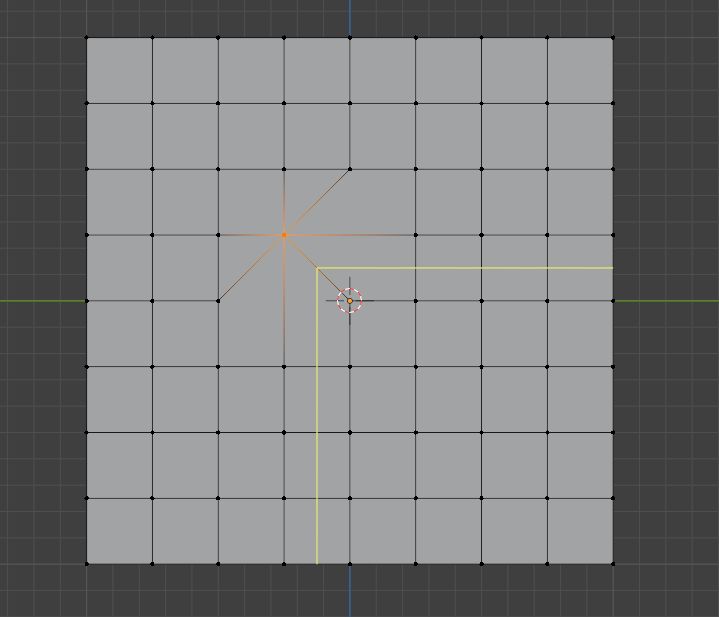
这个技术甚至能让你拐很多个弯
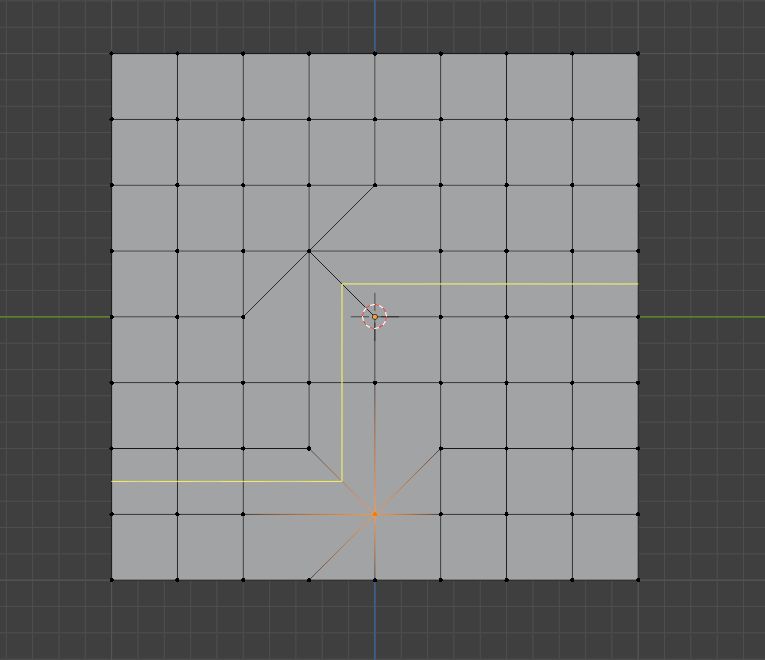
但就如同生活一样,不是所有的消息都是好消息,现在我们不仅有了非四边面,甚至还有了极点
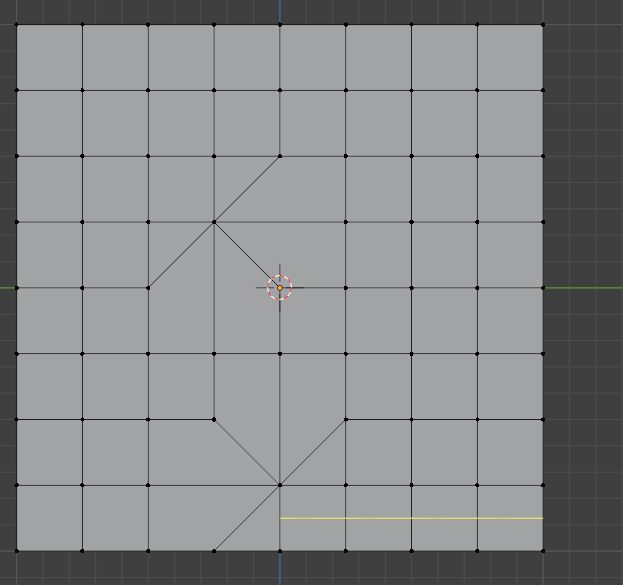
这种超过六条边(包括六条)的极点被称为复杂极点,因为其包含的结构太多,改起来需要耗费不小的精力
不过好消息是,blender可以很方便的解决这个问题
我们只需要选择这些边然后融并即可
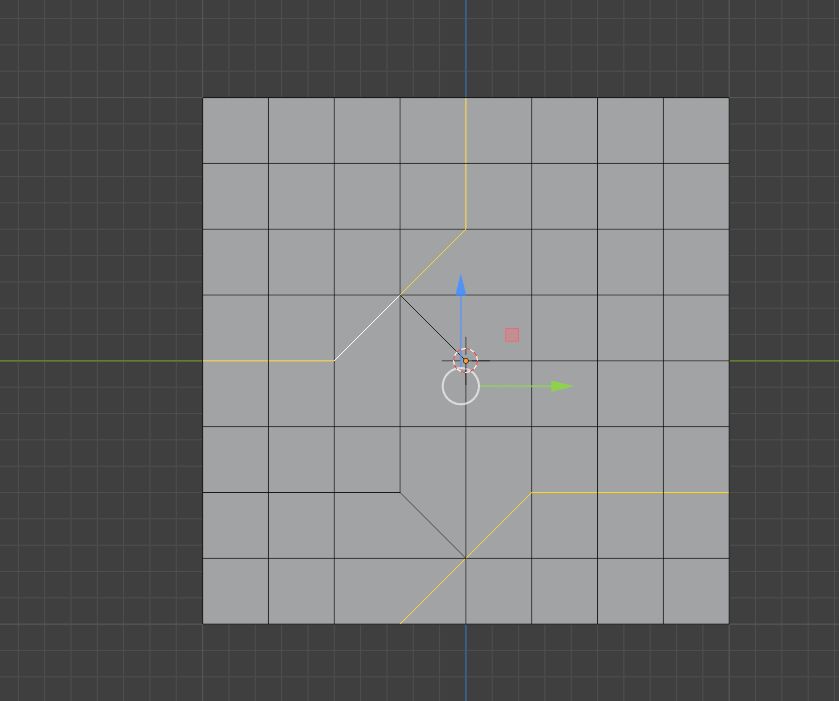
如图所示
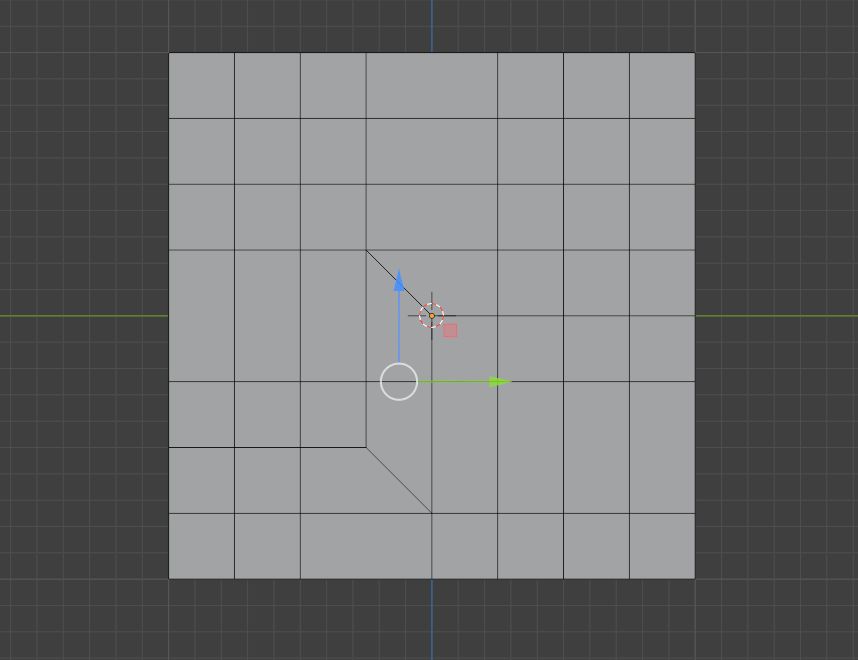
此时我们就可以制作出一个曲线切边路径
但很快我们又发现了新的问题,那就是这个布线的结构并不是很稳固,而且我们的面也变少了,这其实还是给我们后续的工作带来了麻烦
旋转边式曲线切边路径(拓扑斜角均匀)
回到我们原来的模型上,我们必须找到一个尽可能不改变布线结构的做法
于此:我们还是可以使用一开始的旋转法
选中我们要拐弯的地方
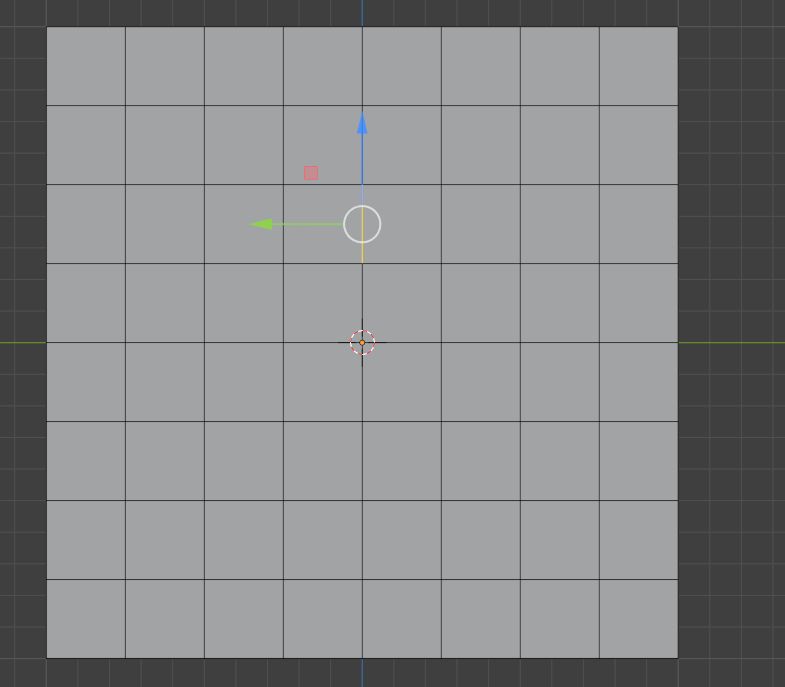
然后融并掉
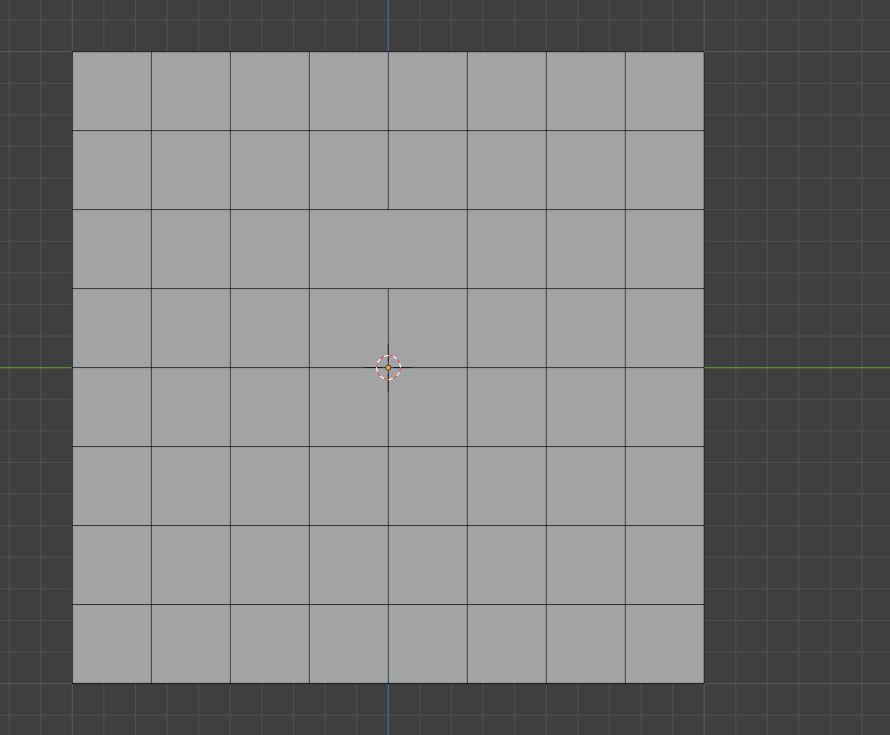
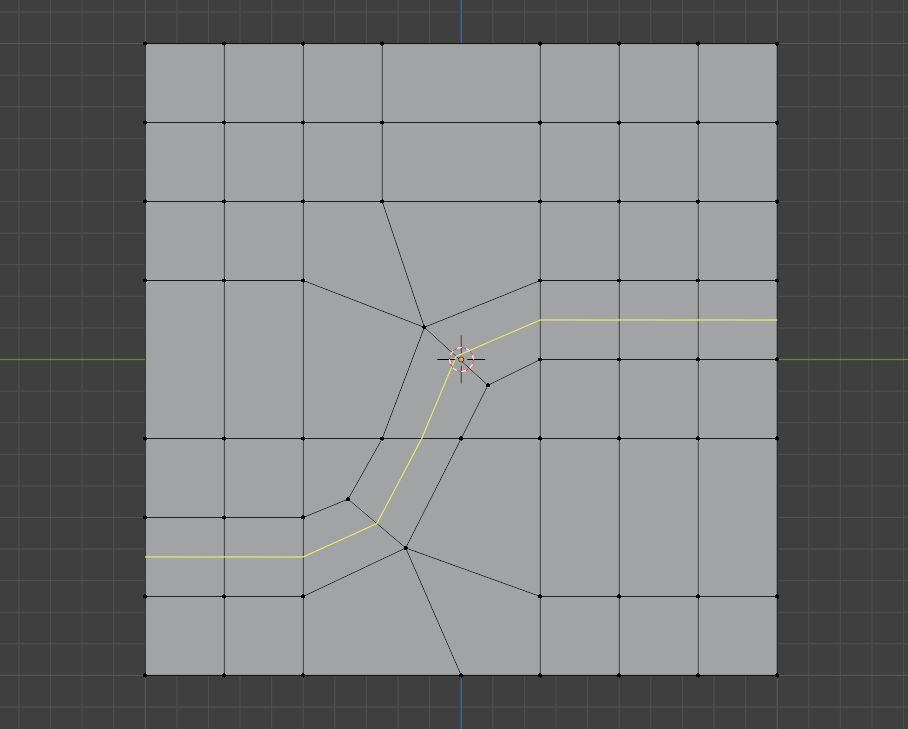
然后将对角顶点链接,看起来就像是刚刚融并的边旋转了一样
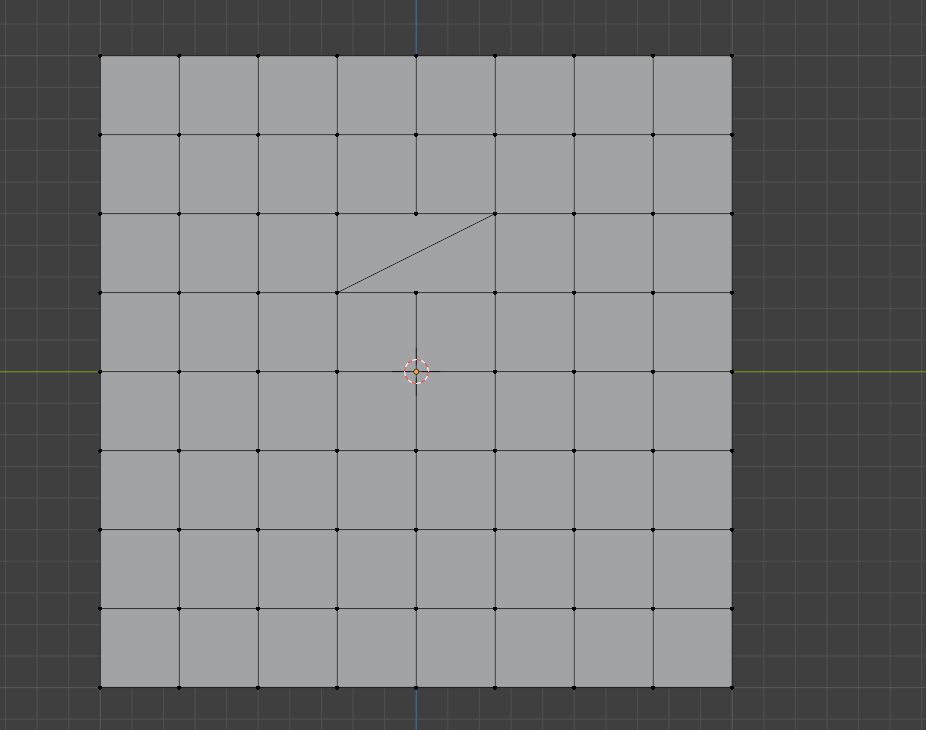
调节一下,我们就可以制作出曲线切边路径
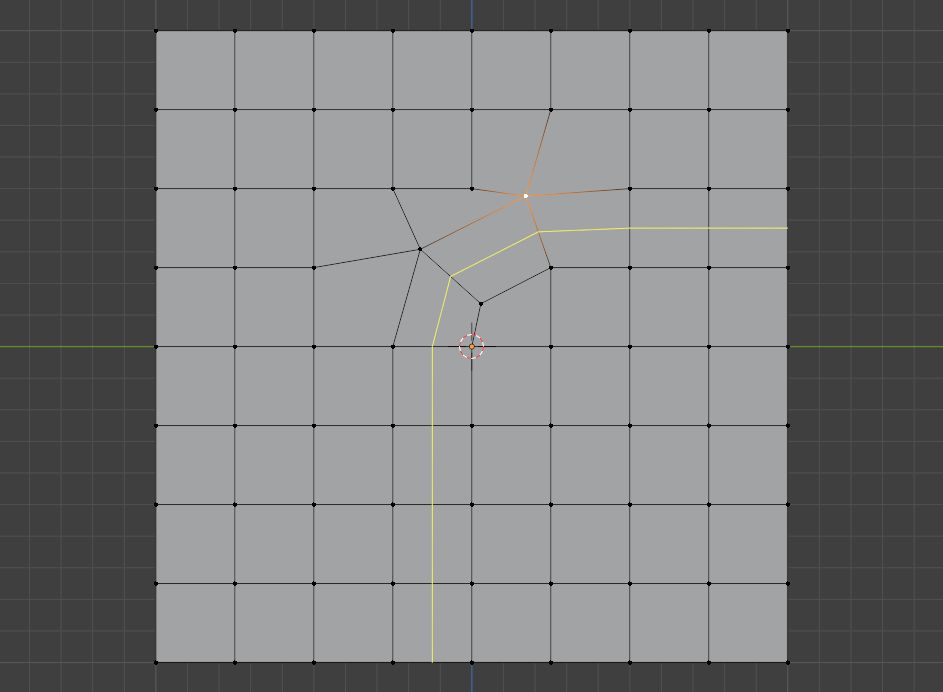
当然这一招并不是完全好用的,毕竟他依然创建了两个极点
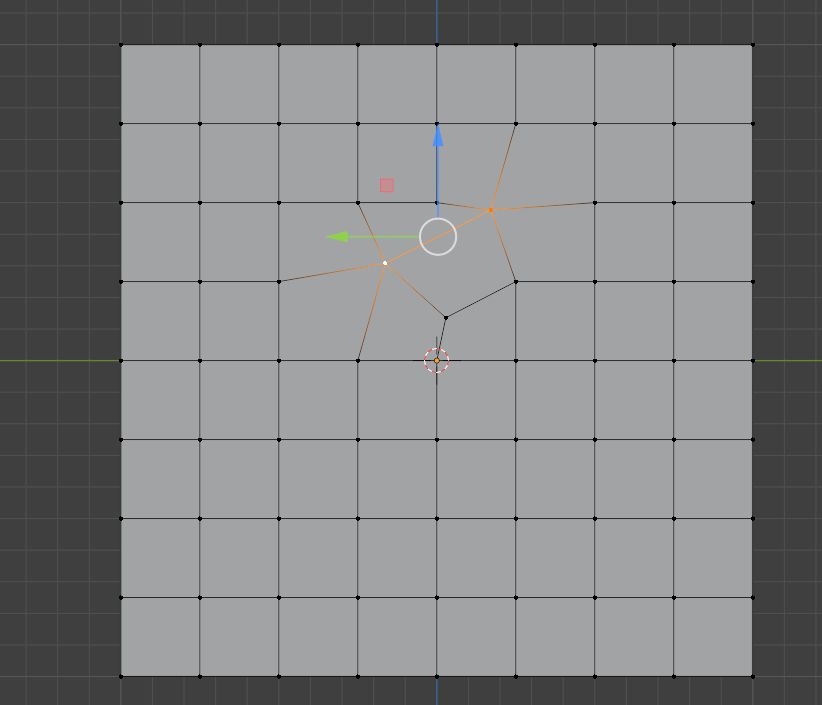
并且它依然打乱了切线走向
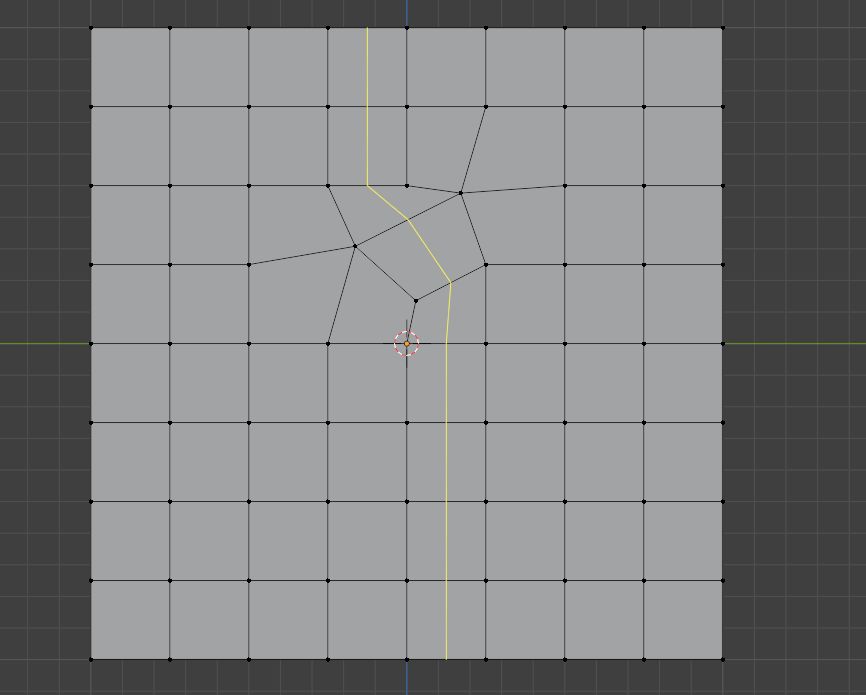
不过好消息是这种切线路径是可以预测的,起码不会断断续续了,也不会出现复杂极点了
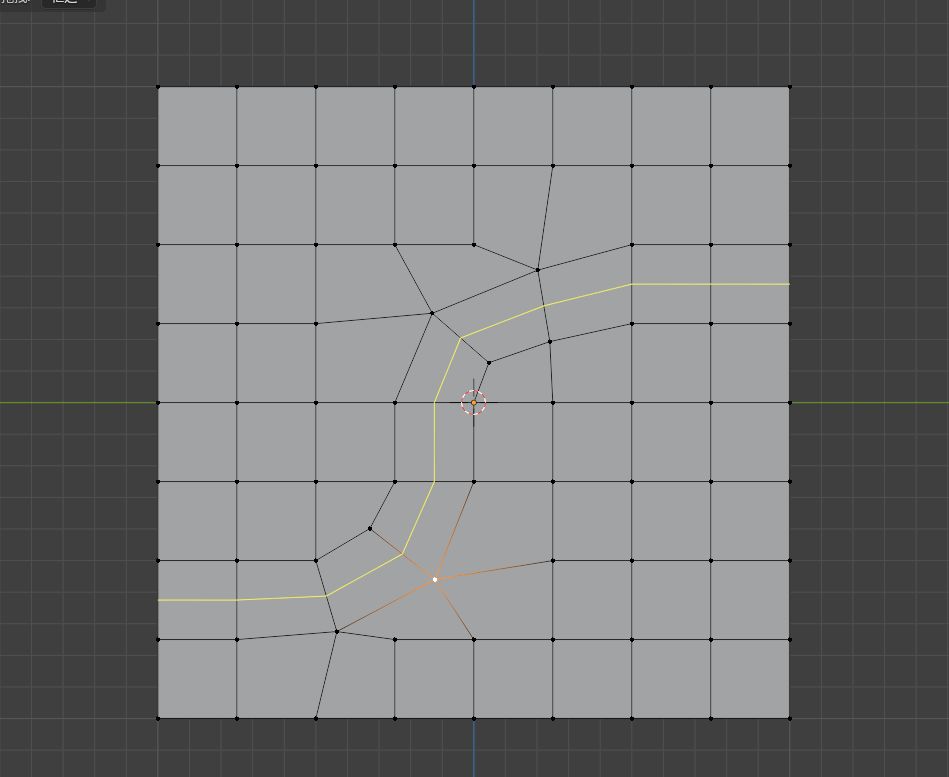
这种操作在弯曲的时候也不会出现严重的失真
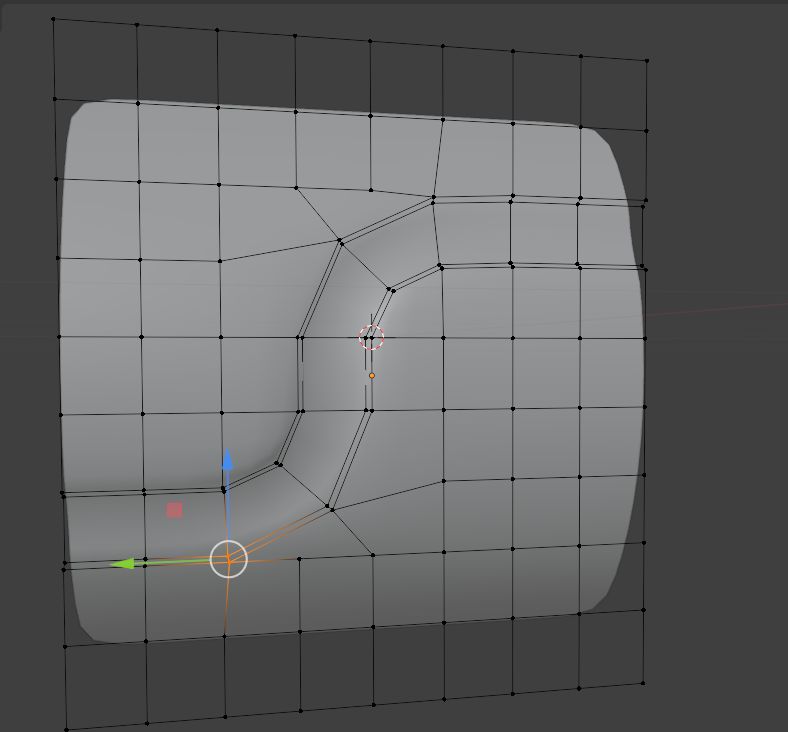
可以看到效果不错

不过有时候还是会有很多问题,因此我们需要用旋转操作进行调整
选择极点的其中一个边
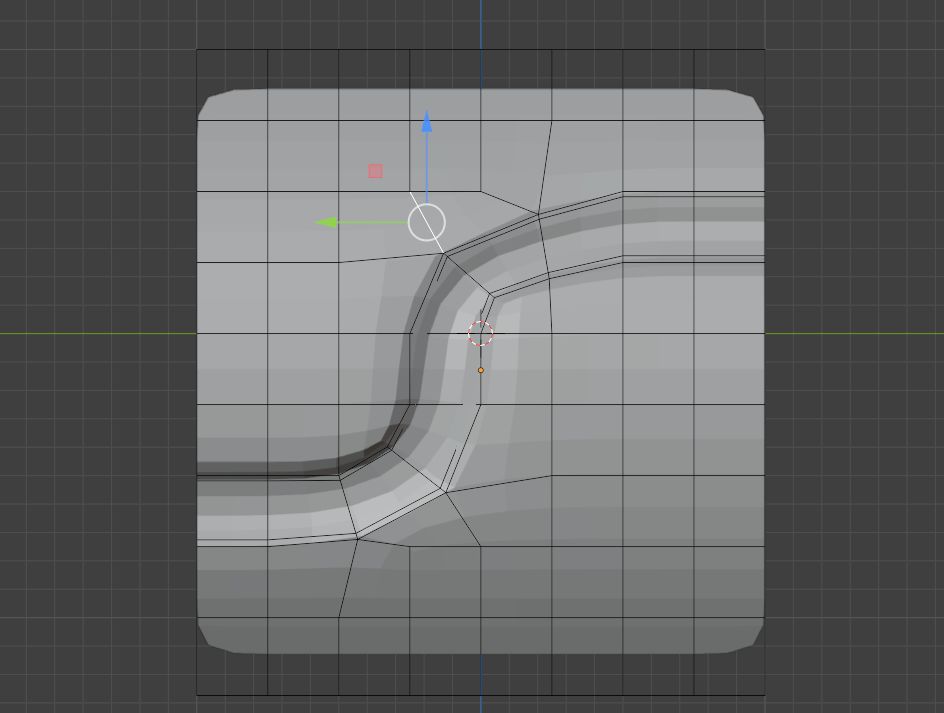
融并掉
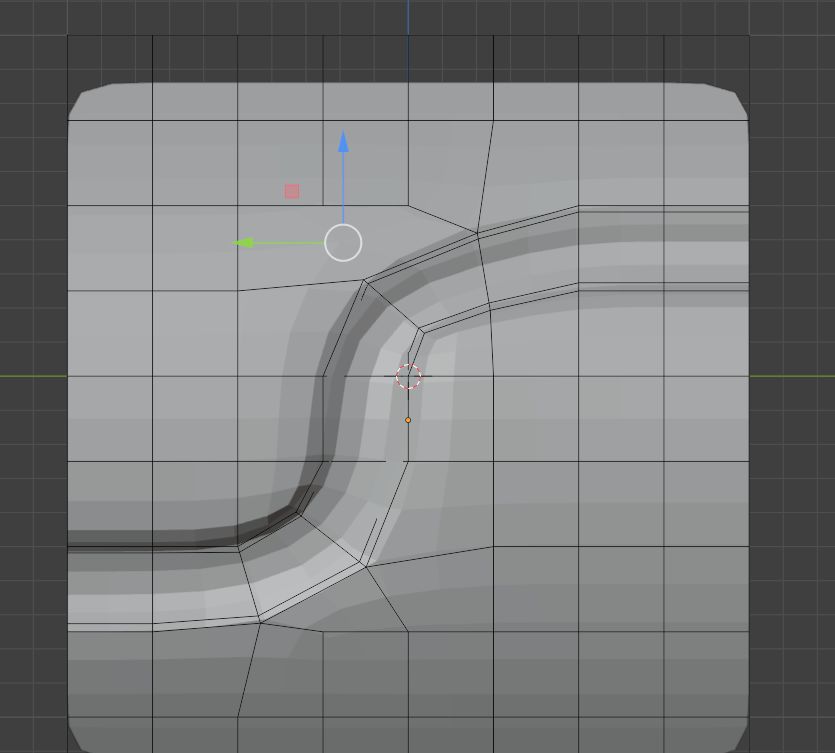
然后链接对角顶点
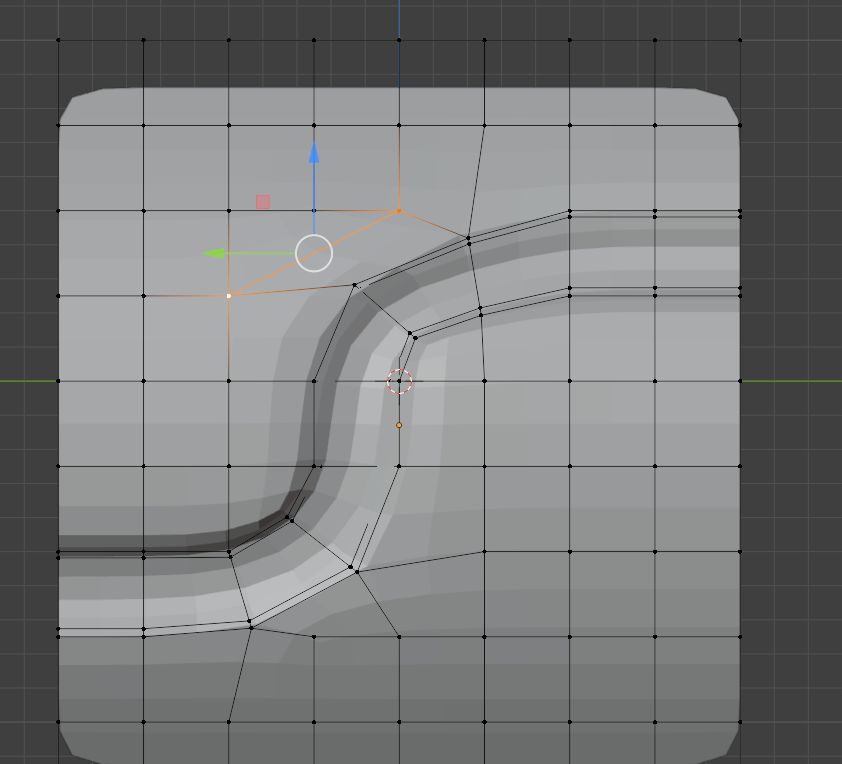
这样处理之后,极点就消失了,我们的模型在后续就不会再出现奇奇怪怪的问题了

当然,如果你觉得又融并又连接的很麻烦,其实可以直接在这里用旋转边
至于为什么一开始不说,那是为了让大家理解原理(其实就是忘了)
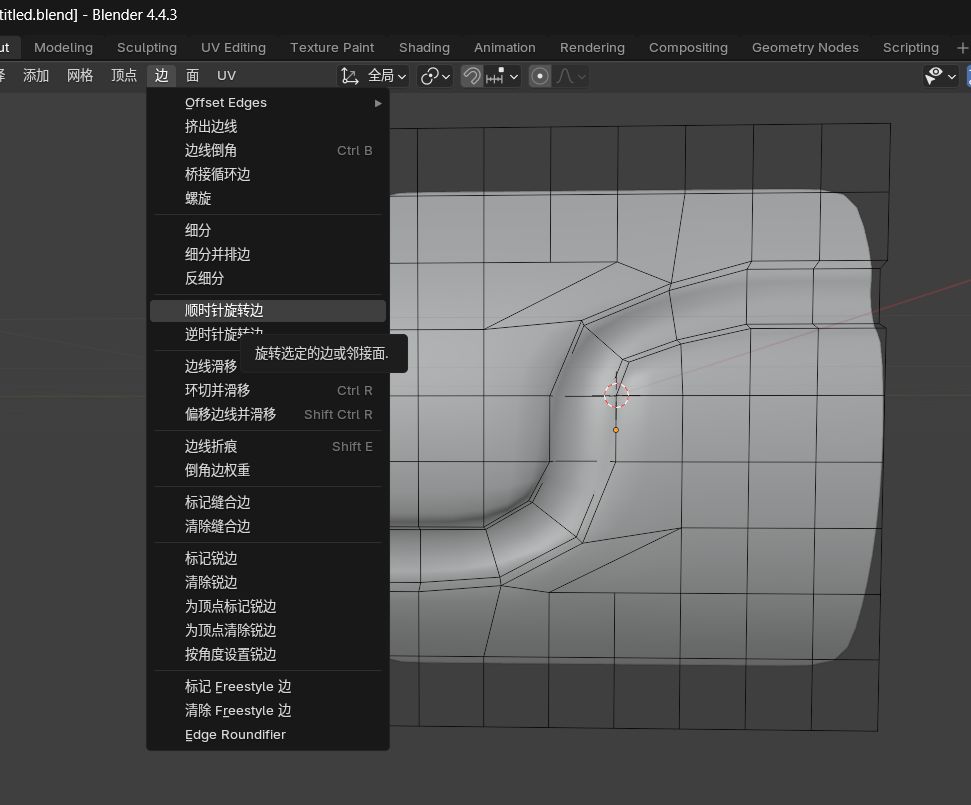
旋转边式曲线切边路径的其他应用:
保护术
当我们有一个不想被切线的部分时,比如这样
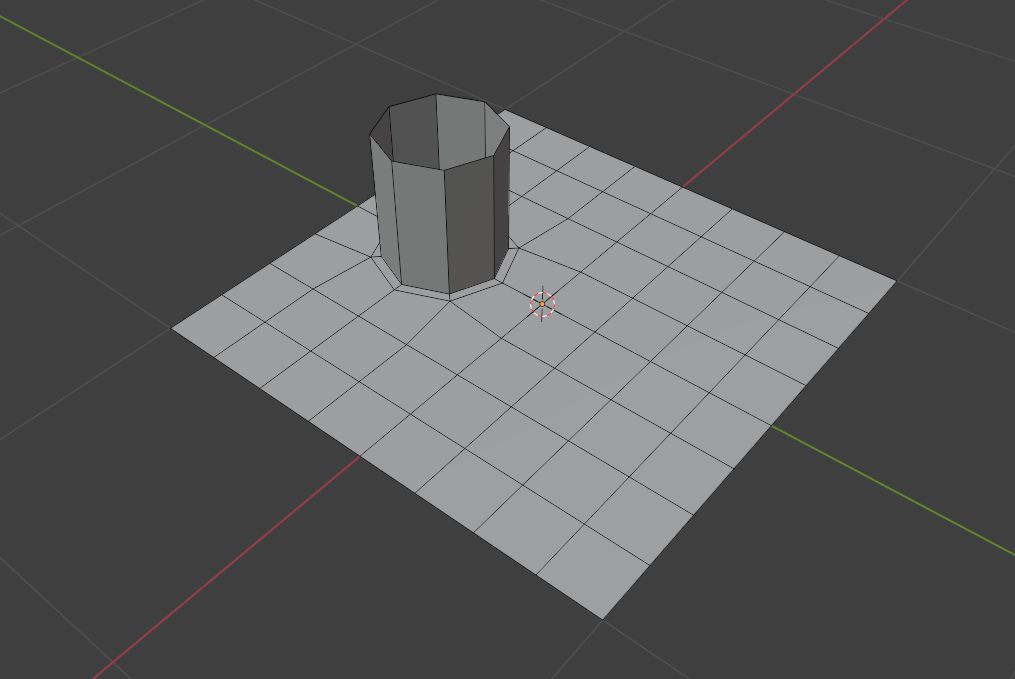
如果我们直接用环切切线,那么你会发现这条线会蹬鼻子上脸到圆柱的位置
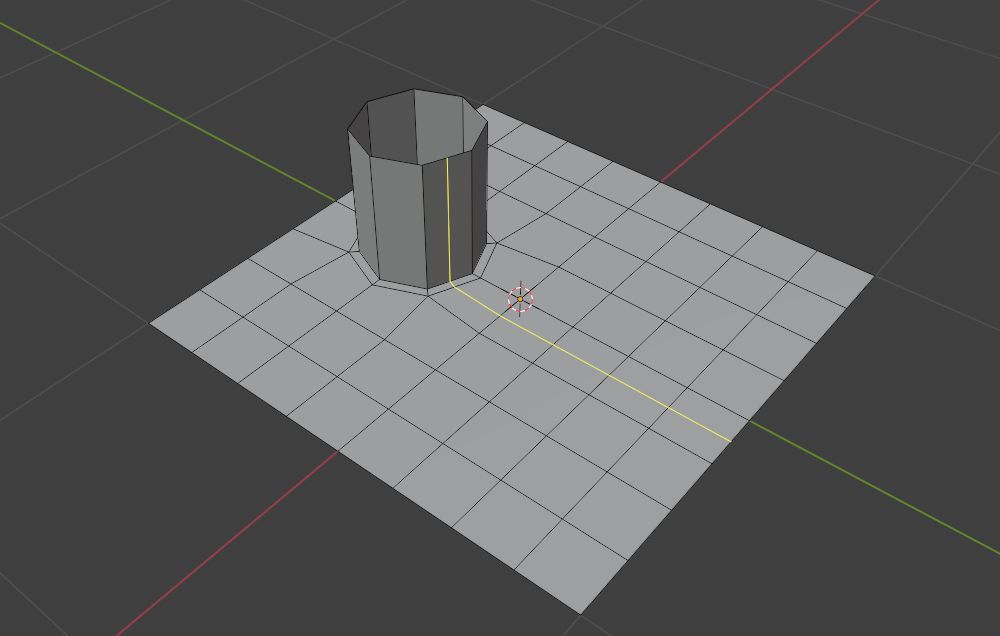
为了防止给我们未来的操作造成困扰,我们可以使用旋转边的方式来处理切线走向
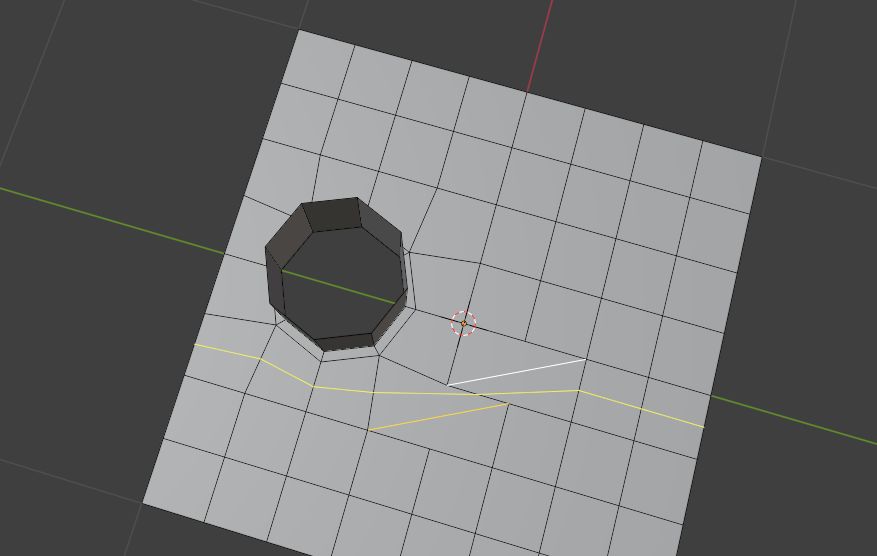
你甚至能绕一圈再回来…
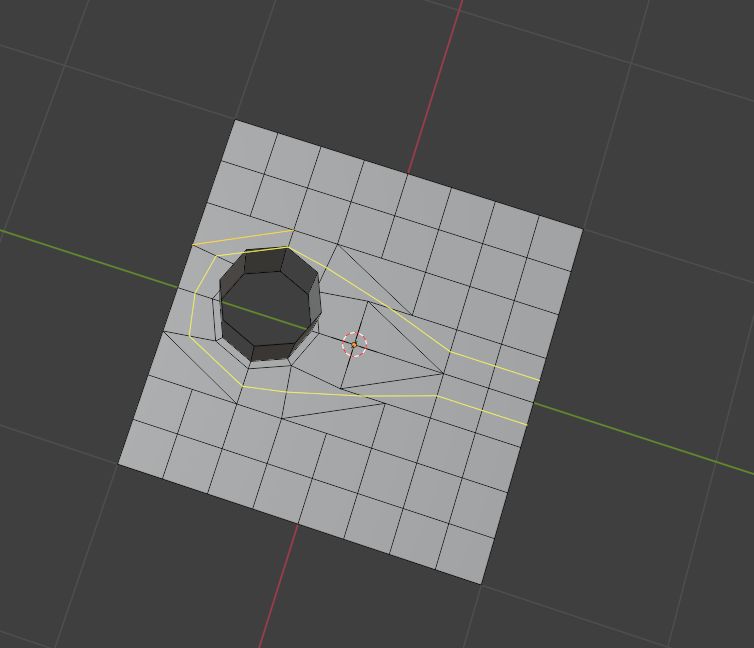
效果非常完美

开门术
除去上述情况,还有一种情况:
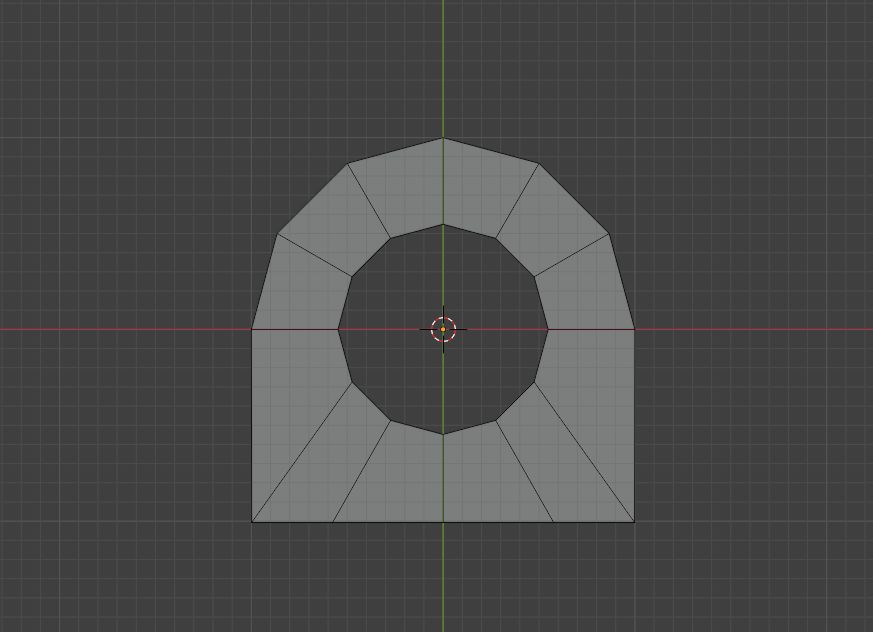
假设我们要为这个模型进行切角,使用环切可以很方便的切一个循环边
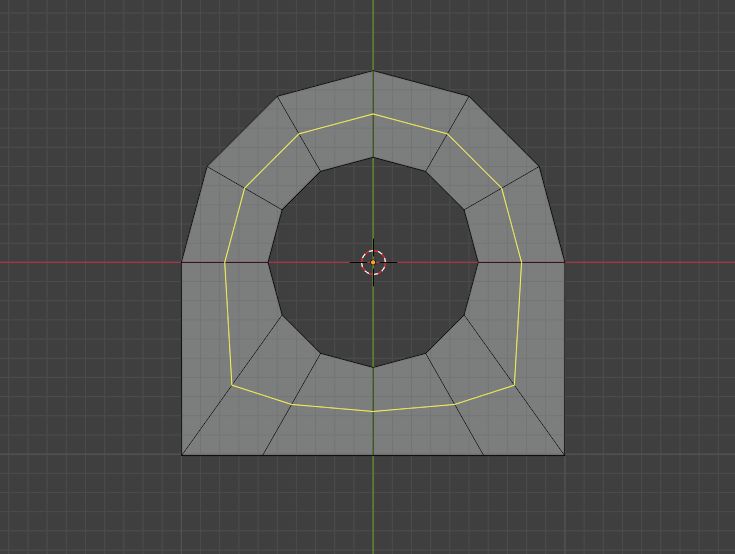
但如果我们的要求是这样呢?
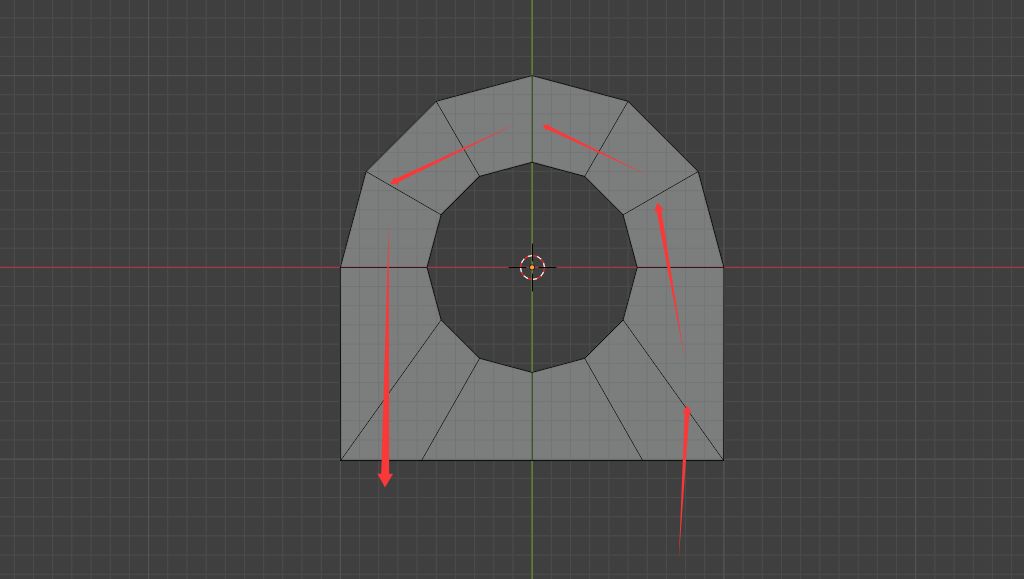
为了制作这个效果,我们可以先挤出一点,搭建一个基础四边面结构
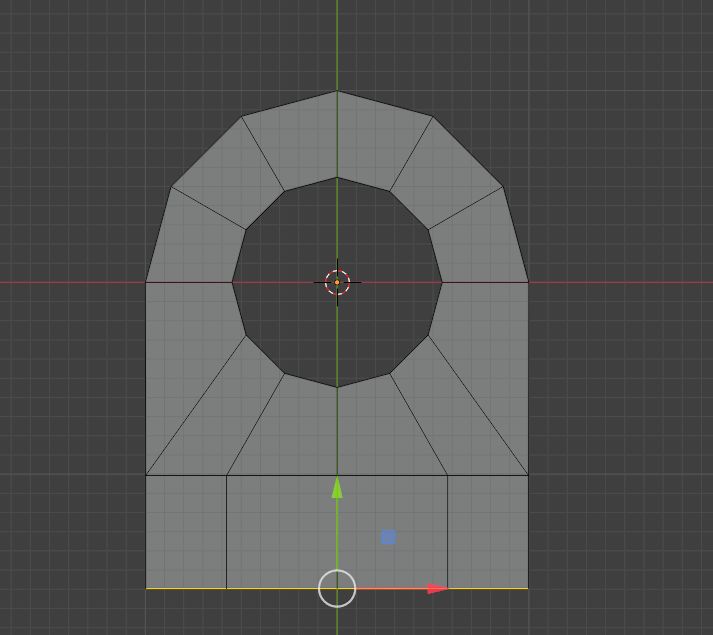
然后旋转这个边
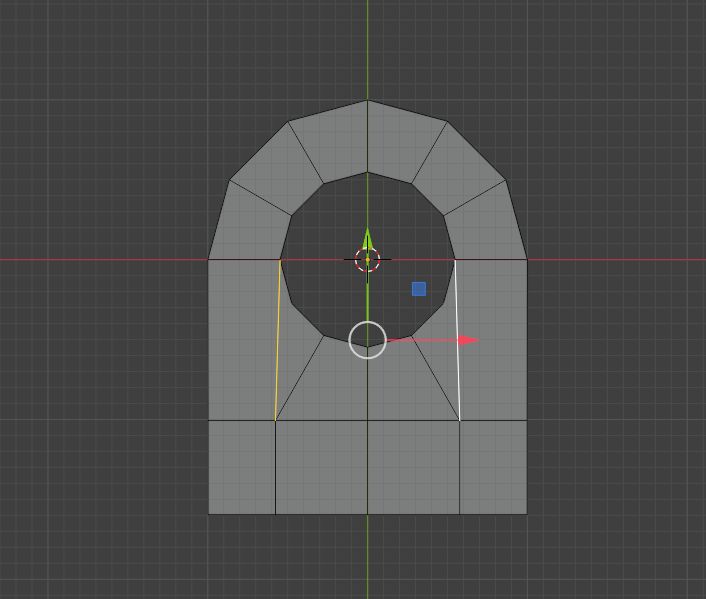
切线走向就正常了,非常完美,形状就像一个门一样s
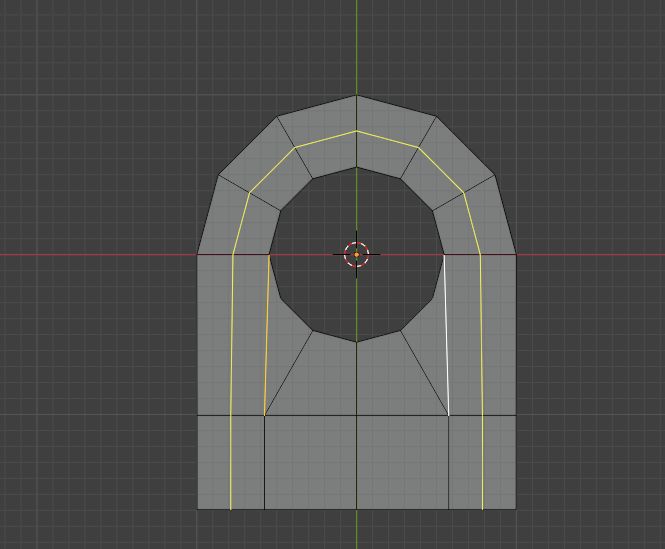
如果你想的话,甚至可以把边转回去
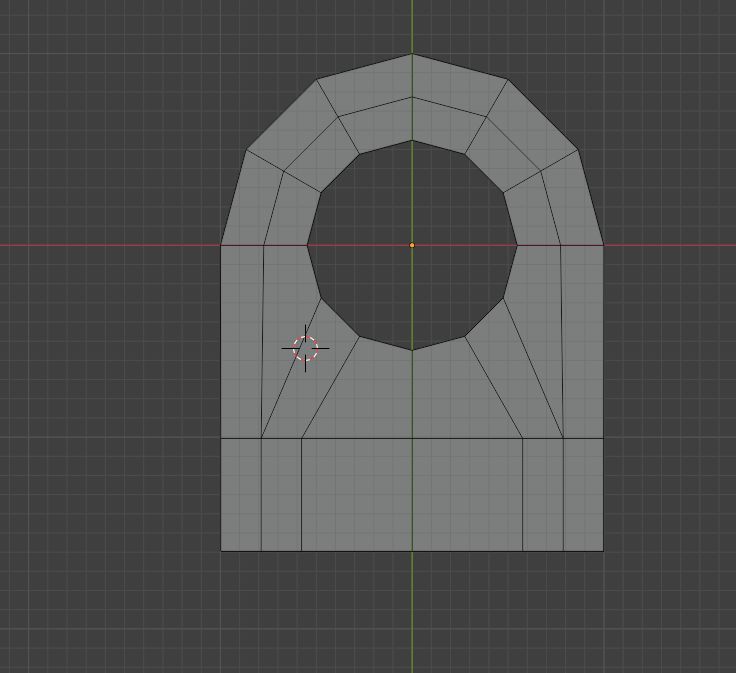
这种操作甚至可以做机械瞄具
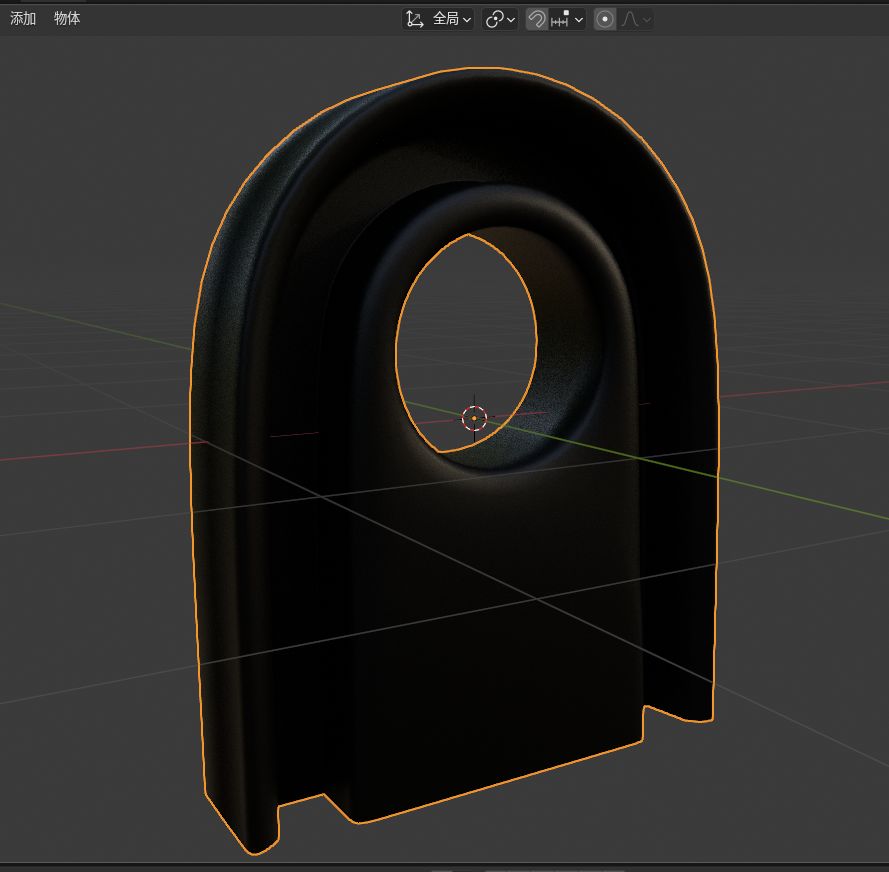
倒角式曲线切边路径
上文我们所说的主要是减面,而接下来我们要学的是加面
选中你要走的切边路径
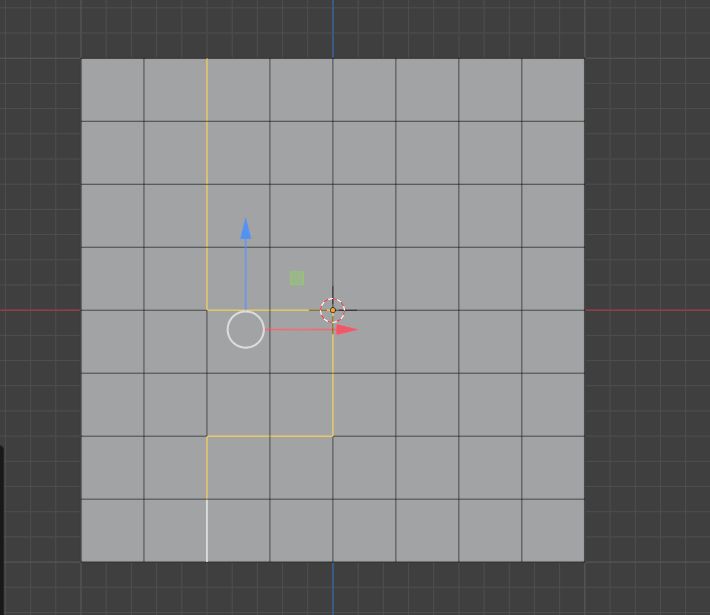
然后倒角,它会给你创造一个切边路径出来
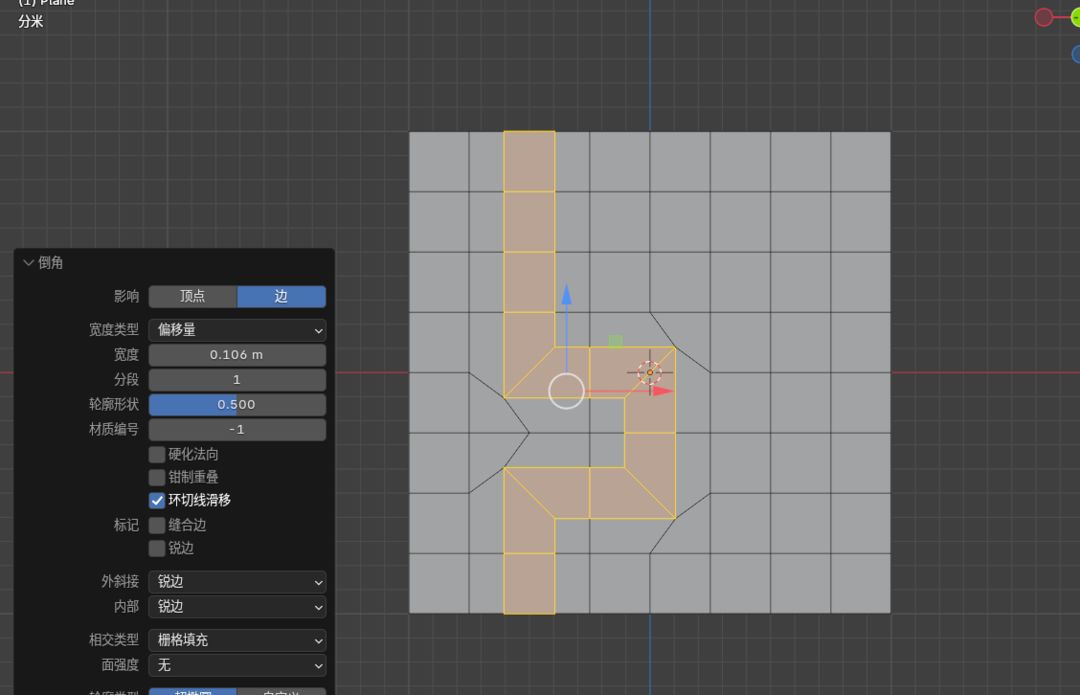
这个方式是最简单暴力的方式,但是乱用的话也会出现很多问题
结尾

