对于奇数阶最优解的讨论

在此之前，有网友给出了一般性解法，不再赘述，下面将使用该方法就奇数阶最优解做以说明。

bd与pq是不同方向的，我们这里只取一个方向。

对于任意n阶,有

1.变换所有行或列则所有字母改变。

2.变换某个字母偶数次，整体不变，即与不改变相同。

3.变换多个不同字母，先后顺序不影响最终状态。

所以，当通过一般性解法找到某一个解时，我们可以根据1.2.3.三条找到另一个解，即除了第一个解的字母外的所有其他字母，它们构成了第二个解。

因为 题目(某个解→)全部b(或d)(1.→)全部d(或b)，

根据2.3.有(某个解→)(1.→)=(第二个解→)

所以假设某个解需要m步(变换m个字母,0<m<n²)，则第二个解需要(n²-m)步，取m和(n²-m)较小值，则对于所有情况来说最多需要n²/2向下取整这么多步就可以解决了。

之后我们发现了这么一个事实:

变换所有行或列→所有字母改变 成立，但

所有字母改变→需要变换所有行或列 不成立

进一步的，对于偶数阶这个结论成立而奇数阶不成立，原因是奇数阶还有一个方法:

4.对于奇数阶，只变换一行或一列，则所有字母改变

这是一个减少奇数阶解法步骤的最有效的一个工具，直接上图，这里用5阶举例

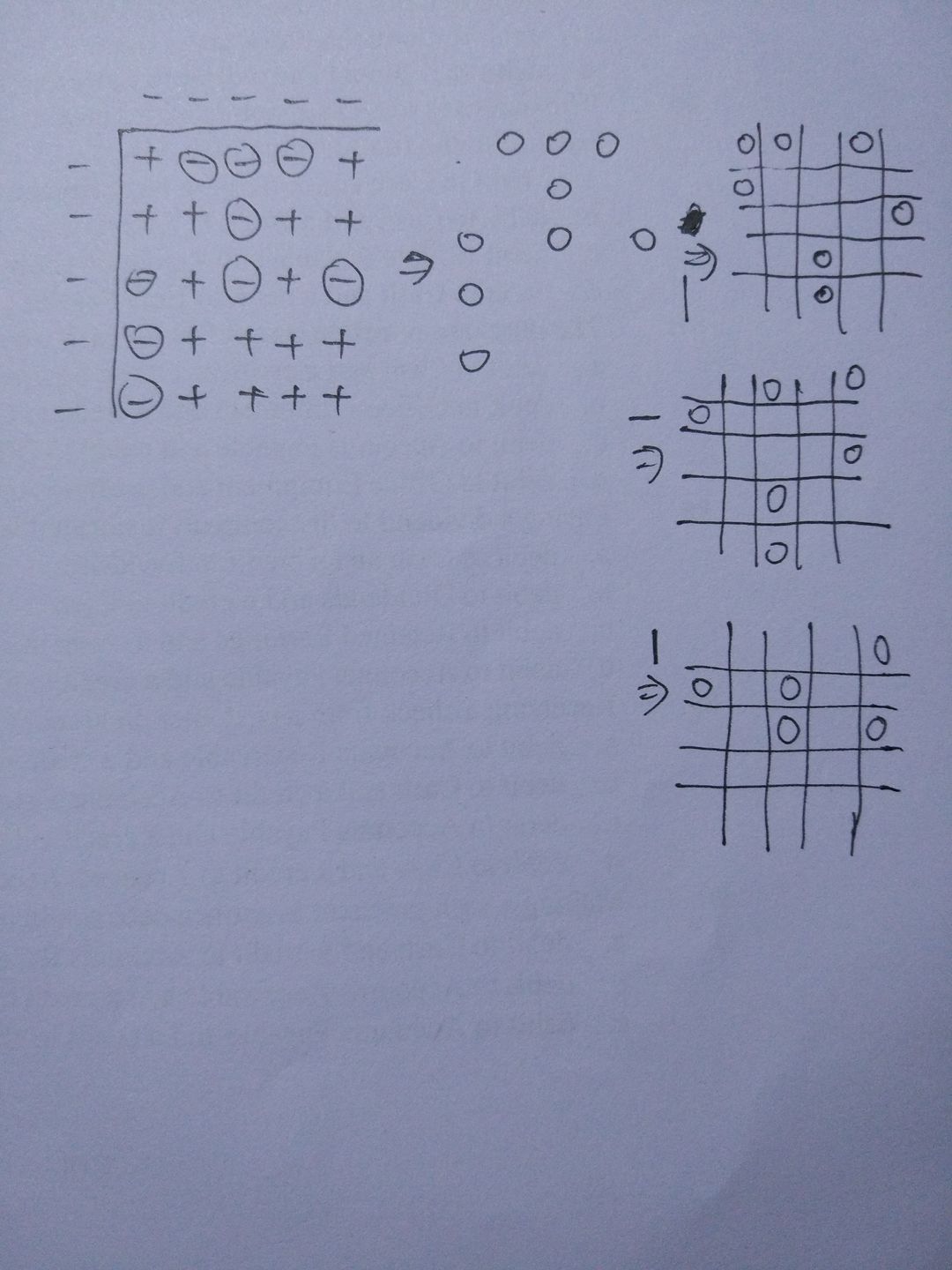
我们可以看到，当奇数阶给了某个解之后，我们只需要把解中某行或某列变换3个及以上字母改为变换这一行的其他字母那么就可以减少步骤，并且根据2.和3.，还可以多次使用这个方法。值得注意的是，一味的使用是有漏洞的，假如有三行以上每行有两个，那么变换1或者2行的两个为三个，则在列上可以消去更多来弥补之前增加的。在手动消去时，能够弥补这个漏洞的方法是在某一个能消去更多的方向上先变换。

严谨的证明正在准备中。。。

欢迎大家一起讨论这个结论。