无保底抽卡期望计算（x）

无保底抽卡期望计算

设期望为E（x）

假设抽中概率为p

未抽中概率为（1-p）

第一次中概率为p

第二次中概率为p（1-p）

第三次中概率为p（1-p）（1-p）

。。。。。。

又因为

E（x）＝xi*pi

所以

An＝xn*pn＝np(1-p)^(n-1)

E（x）即为数列An的前n项和

Sn=

1*p+2*p*（1-p）+3*p*（1-p）²+4*p*（1-p）³。。。。。。np(1-p)^(n-1)

（1-p）Sn=

1*p（1-p）+2*p*（1-p）²+3*p*（1-p）³。。。。。。np(1-p)^n

Sn-（1-p）Sn=pSn=

p+p（1-p）+p（1-p）²+p（1-p）³。。。。。。

p(1-p)^(n-1)-np(1-p)^n

Sn=

1+（1-p）+（1-p）²+（1-p）³。。。。。。

(1-p)^(n-1)-n(1-p)^n

第一项到倒二项构成一个等比数列，设其为Bn

B1=1 q=（1-p） 总共n项

设Bn前n项和为Tn

Tn=

｛1［1-（1-p）ⁿ］｝/｛1-（1-p）｝

=［1-（1-p）ⁿ］/（p）

Sn=E（x）

［1-（1-p）ⁿ］/（p）-np(1-p)^n

假设p为0.01（也就是精s成功率）

Sn＝100-（1+0.0001n）（0.99）ⁿ

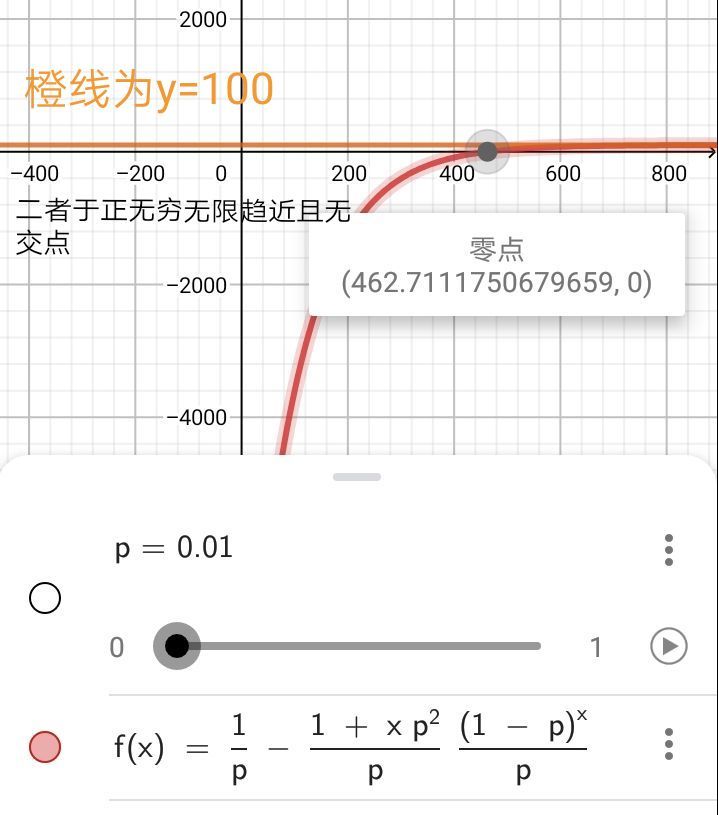
即期望无限接近100

也就是说精s平均要100抽才能完成

因此

E（x）期望可默认无限接近但小于（1/p）

我就是很闲orz