[数据分析]50抽之后到底每抽递增多少概率?
修改于2022/09/02689 浏览综合
本文出于兴趣和写给[格_式_化]老哥看的,算错了请指正,欢迎讨论!
参考资料:
高中概率论,以及NGA老哥的excel公式。
官方给的卡池综合概率(含保底)是2.84%,单抽概率是2%,50抽之后每抽概率提升,我就很好奇这个概率提升是多少
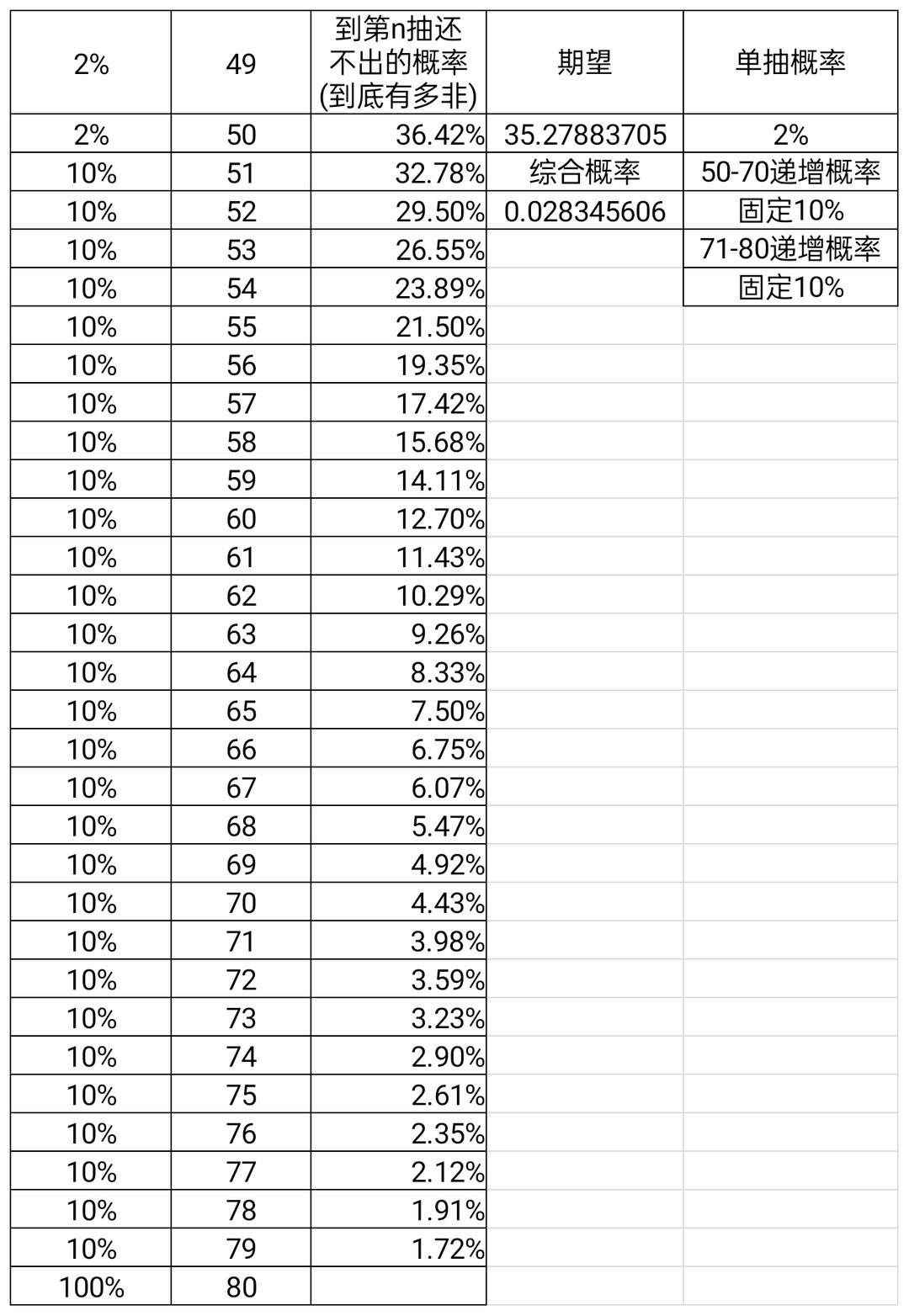
初版结论是51-80抽每抽递增1.3%,79抽时概率40%,最后一抽100%,吃保底概率0.02%,不太符合个人体感,详见最后总结和反思。
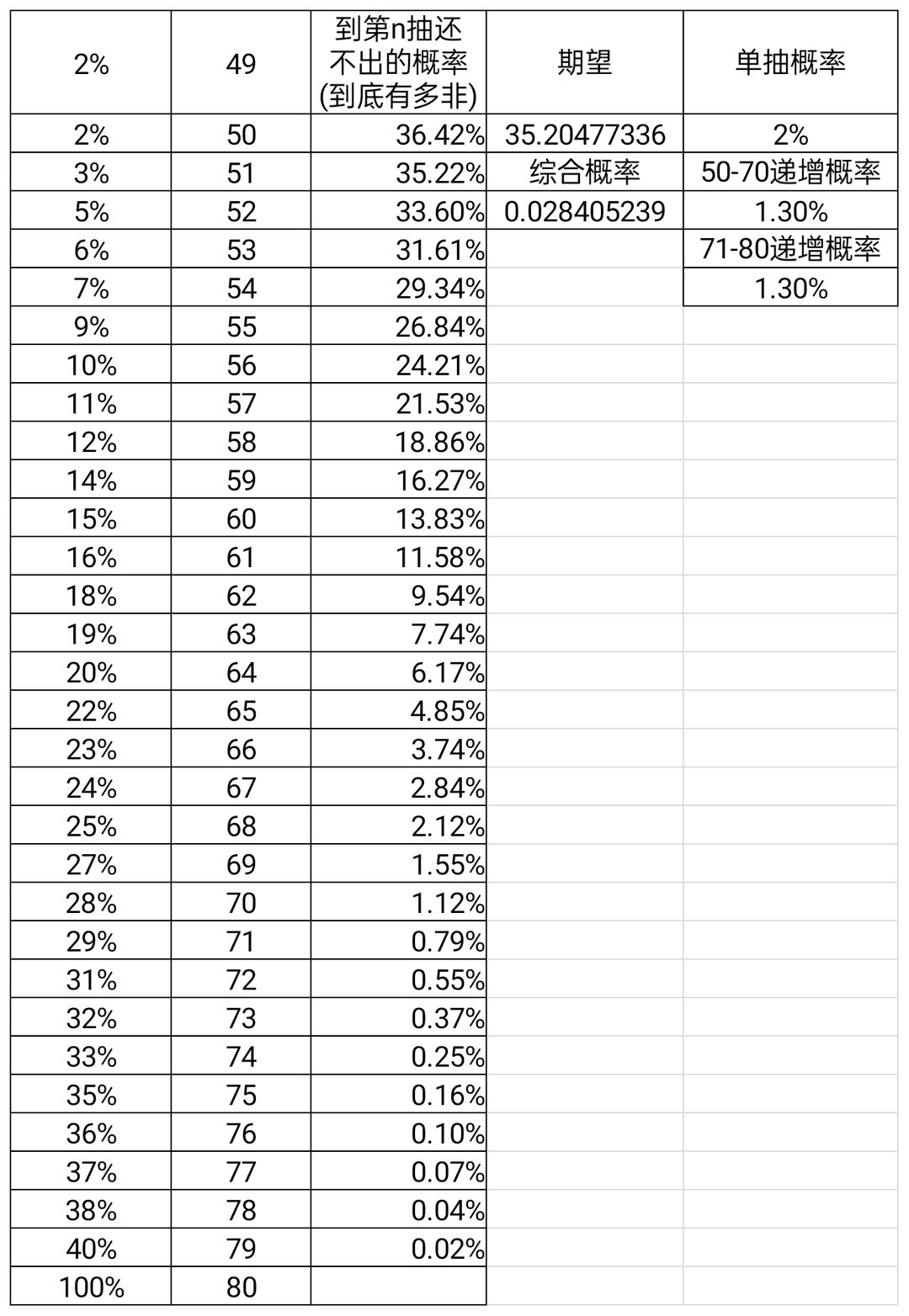
9.2新增:1-50抽2%,51-80抽10%的分布,保底概率从0.02%上升到了1.72%,更符合体感,我更倾向于这个(感谢2楼大佬模拟)

[可忽略,直接看总结]
这里假设每次递增的概率是相同的X,并用综合概率2.84%,即综合期望35.2%倒推X。
1.设事件为抽出一狂就停,则出狂需要的抽数期望应该=(第n抽出狂的概率*抽数)的总和
n为1-80(80就保底了一定会停)
2.前50抽出狂的概率很好计算,因为单抽概率都是2%,所以第一抽是2%,第二抽出是(1-2%)*2%,第三抽出是(1-2%)^2*2%
这里的(1-2%)^n-1是指我前面n-1抽都没出,不然我就停了,不会发生这个事件。
注:(1-2%)^n指(1-2%)的n次方。
表格如下(1-50抽,篇幅限制不全展示)

第三格所用公式:

3.第51-79抽,每抽开始概率递增X,这里先使用我一开始猜想的3%。
前面50抽累计不出的概率是(1-2%)^50。然后另外起三列用于统计51至n抽的累计不出概率,其中黄色格子=自己左边和上面格子的乘积。

使用的公式:

4.最后第80抽概率直接设为1,因为触发保底

5.计算综合期望,将第二列第三列的乘积累加即可,即累加第四列(1-80)。
综合概率=1/综合期望。我们的目标是综合概率=2.84%,让我们来看看递增为3%时的结果:

多了,所以将3%往下调。
2%的结果:

再往下调,最后在1.3%的时候我看到了目标

6.总结:
1-50抽概率2%,51-79抽概率每抽递增1.3%,79抽时概率为40%,80抽时概率为1,此时综合概率为公示的2.84
最后看一下50-80抽才出货的概率吧。仅供参考,因为都是我一个人算的,而且假设的也很简单,错的话请指正!
50抽:36%
60抽:13.83%
70抽:1.12%
吃保底的概率是0.02%。
7.反思
由于我本人触发过70,论坛也见到不少70和保底才出的,所以目前怀疑概率不是恒定递增,毕竟恒定的话官方干嘛不公示呢。
新增:1-50抽2%,51-80抽10%的分布,保底概率从0.02%上升到了1.72%,更符合实际一些,我觉得可以认为是实际模型,可能会细拆成50-60 10% 60-80 11%之类的,但大差不差
50抽:36%
60抽:12.70%
70抽:4.43%
保底:1.72%