关于珍品阁抽奖出货期望的探讨

我曾经发过一篇关于珍品阁期望计算的水贴，现在发现那时候用的计算方法不适用于保底抽奖，而且返还珍品券的情况也没有考虑到，所以计算出的期望是不准确的。

现在我学到了一个计算保底抽奖出货期望的方法，还有计算工具也升级了，所以想重新算一次。

活动规则如下图，已知抽一次抽到珍品券的概率为0.15，抽一次返还64江湖令的概率为0.2。如果前14次都没有抽到珍品券，则第15次至少获得一张珍品券，即保底，同时清空抽奖进度。

先计算抽奖次数对应的出货数，所用的方法是，设抽奖次数为n，第n次抽到珍品券概率为x，没抽到珍品券的概率为1-x，则第n次对应的变量公式是n*(1-x)^(n-1)*x，第15次是保底，对应的变量公式是n*(1-x)^(n-1)，计算出前十五次的变量和，出货数期望就等于抽奖次数与变量和的比值，即抽奖次数与变量和倒数的乘积。

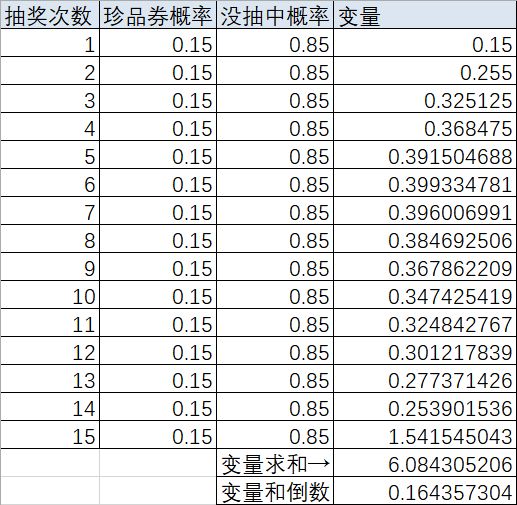
这里x=0.15，变量和等于∑（i=1，n=14）[n*(1-0.15)^(n-1)*0.15] +15*(1-0.15)^14≈6.084305206，所以抽奖1次，出货数期望值等于1/6.084305206=0.164357304，抽奖n次，出货数期望值等于n/6.084305206=0.164357304*n，这是考虑保底但是不考虑返还江湖令的情况下的出货数期望值。当n=5，即进行一次五连抽时，出货数期望值为0.821787。

那么一张珍品券需要的江湖令期望值是多少呢？江湖令期望值等于变量和与抽一次所需江湖令数量的乘积，等于6.084305206*80=486.7444165江湖令。

然后来考虑返还珍品券的情况，珍品券的返还没有保底，所以计算方法可以简单一点。

为了简化问题，我设抽奖分为几轮，假设第一轮抽奖全部用原有的江湖令，第二轮抽奖用第一轮抽奖返还的江湖令，第三轮抽奖用第二轮抽奖返还的江湖令，以此类推，最后返还的江湖令越来越少，不足以进行下一轮抽奖的时候，抽奖停止。

这样算有什么好处呢？可以利用上面的公式，分开计算原有江湖令和返还江湖令对应的抽奖次数和出货数。

设开始抽奖时江湖令数量为p0，一般有两种抽法，一是全部单抽，二是全部五连抽，设第一轮抽奖次数为n0，单抽次数为int（p0/80），五连抽次数为int（p0/400）*5，这里int是括号内的公式的计算结果向下取整，

即n0=int（p0/80）或int（p0/400）*5

第一种抽法是当江湖令数量小于80时结束，第二种抽法是当江湖令数量小于400时结束。

先计算返还江湖令数量，这里直接用抽奖次数与概率的乘积来计算期望，返还江湖令期望数=每轮抽奖次数*返还江湖令的概率*返还江湖令的数量，所以返还的江湖令数量p1=n0*0.2*64=12.8*n0=12.8*(int（p0/80）或int（p0/400）*5)

然后计算返还的江湖令对应的抽奖次数，即下一轮抽奖次数，抽奖次数公式在上面，把开始抽奖时的江湖令数量p0换成返还的江湖令数量p1，所以第二轮抽奖次数n1=int（p1/80）=int（12.8*n0/80）或int（p1/400）*5=int（12.8*n0/400）*5

然后计算抽奖次数对应的出货数期望值，第二轮出货数期望值等于0.164357304*n1

最后再计算抽奖次数返还的江湖令数量，接下来要进行的步骤是重复上面的循环，直到江湖令用完，抽奖全部结束。然后计算出每轮的出货数期望值，最后求和，即得到考虑返还江湖令情况下的出货数期望值。

接下来考虑江湖令用完，抽奖停止的情况。原有江湖令数量决定了抽奖总次数，当初始江湖令数量不多的时候，返还的江湖令期望数不足以支持第二轮抽奖，抽奖停止。

比如对于单抽来说

当12.8*n<80，12.8*int（p/80）<80，p<560时

第一轮江湖令数量小于560时，抽奖次数小于7次，此时第一轮返还的江湖令期望数量小于80，抽奖停止。

接下来的情况同理，限于篇幅就不一一列举了，下面直接用计算工具给出实例。

我制作了一个表格，输入江湖令数量可以通过上面介绍的方法模拟计算出期望抽奖过程和抽奖结果。

实例1,559江湖令。

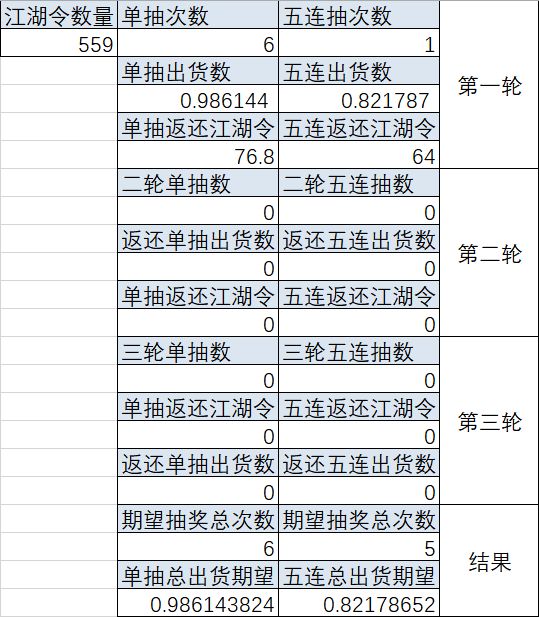
实例2，3000江湖令。

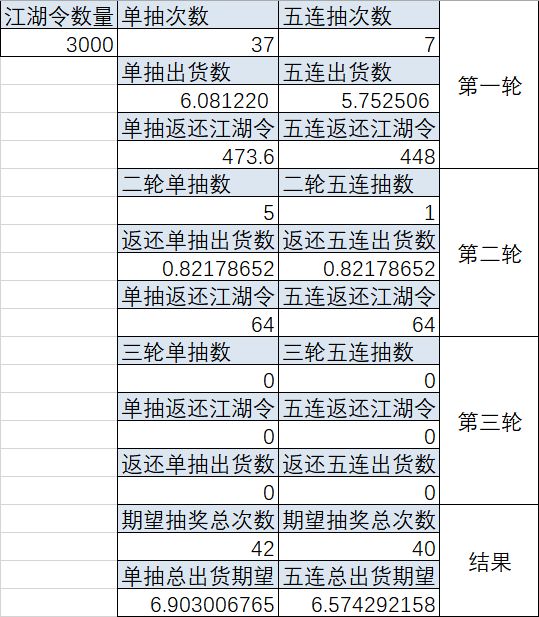
实例3,60000江湖令

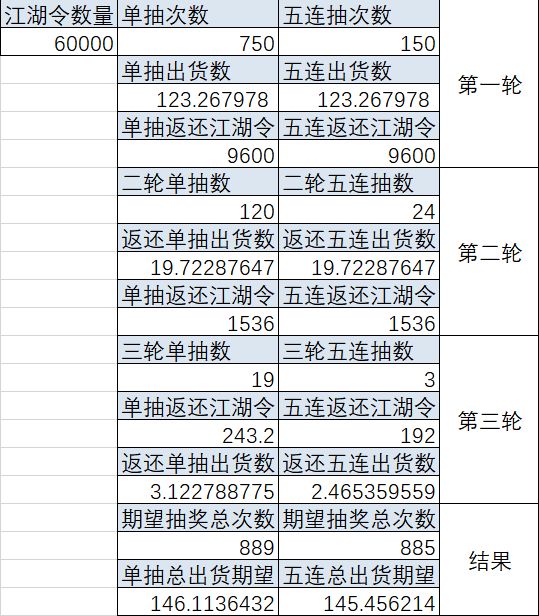
将三个实例的总出货期望除以期望抽奖总次数，你会发现结果都极其接近一个值，那就是0.164357304。

还记得上面不考虑返还江湖令时，得出的结论吗？抽奖n次，出货数期望值等于0.164357304*n，而我们现在考虑了返还江湖令的情况，出货期望数与抽奖总次数的比值却仍然几乎没有变化，这是不是可以说明，返还珍品券并不影响抽出一张珍品券需要的江湖令期望值和抽奖次数与出货数期望值的比值，只是增加了抽奖次数，相应增加了出货数量呢？

所以在考虑返还珍品券的情况下结论仍然不变，也就是说，平均抽一张珍品券还是需要486.7444165江湖令，抽奖n次，能抽到的珍品券数量期望是仍是0.164357304*n