为什么非酋总是存在？而且看起来很普遍？

2023/08/1329 浏览综合

假

设某奖池中奖率p%，买100抽，中奖次数期望为p。那么抽彩票的人总会有一个预期——100抽应该出p个。

现在姑且认为每次抽奖重复独立，即每次抽概率都相等，各次抽奖都不会影响其他的抽奖结果。这100重伯努利试验中中奖次数记为X。P(X=0)=(1-p)^100。

当然我们可以通过按计算器的方式算出这个该死100次方，但是有个更好的办法——利用泊松分布来逼近结果：

泊松分布中中奖次数为k时的概率，其中的Lambda为常数（垃圾，连希腊字母都打不了）

设n*p=Lambda，二项分布在n趋向于无穷时：

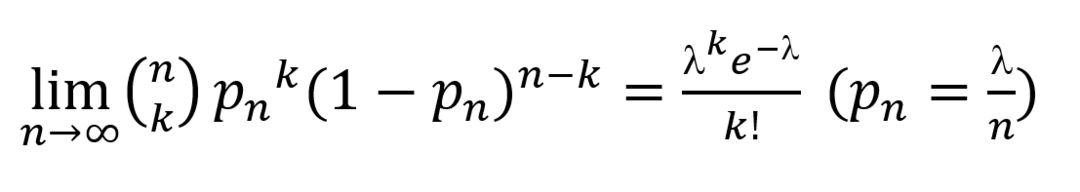
公式

由于n*p=Lambda，当n很大（超过20）时，p很小，就可以近似的认为：

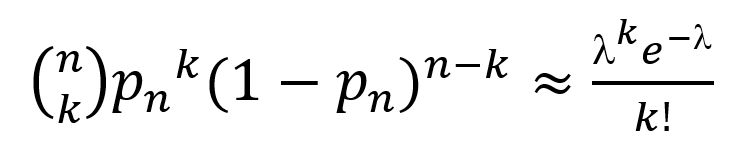
公式

据上面的近似计算，什么都没有的倒霉家伙P(X=0)=1/e=0.37；

至于超过三个的幸运儿P(X>=3)=1-P(X=0)-P(X=1)-P(X=2)=0.08。

下次抽不到还是认了吧，毕竟看起来还满常见的。