当我尝试用数学的视角看抽卡

8 小时前3 浏览综合

作为崩铁和粥双料欧皇，以前我对抽卡游戏的心态一直平和宁静，什么up不up的只要我出手结果只有被我收入囊中。

但是在最近经历了妮姬国服的230抽未出桃乐丝的耻辱性大败之后，我为了调整自己的心态，试图用数学的角度去分析在此类游戏中抽卡的概率，来看看我的运气究竟有多差，于是我就运用高中学过的数学来进行计算：

首先我们明确一点，妮姬池子没有保底，且抽出ssr的概率为4%，在这4%中抽出桃乐丝的概率是1%，也就是说每一抽都是恒定1%的概率抽出桃乐丝。

那么如果我需要计算至少出一次桃乐丝的概率，那么我只需要算出一次也不出的概率，再用1去减就可以了，因为至少出一次和一次也不出是互补事件

也就是说 P（至少出一次桃乐丝）＝1-P（一次也不出桃乐丝）^n（抽取次数）＝1-（0.99）^n

那么我们就可以按照这个公式得出一个漂亮的函数图

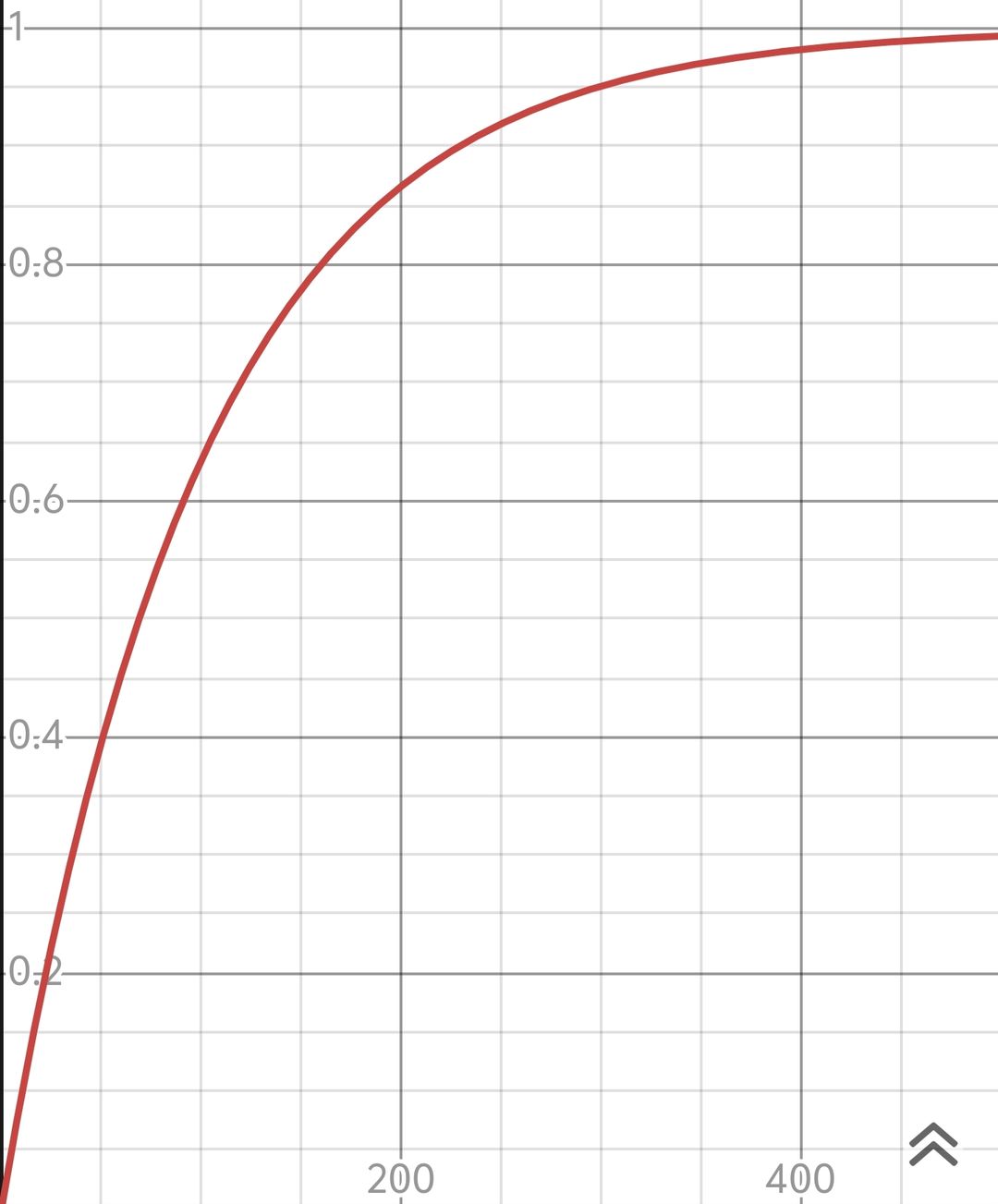
从图像和之前的公式可以知道，50抽时理论出货期望就有39%，100抽时的期望就已经来到了63%，而200抽的期望概率就已经来到了86%

而我230抽才出货对应的的期望概率则是90%，这么看来这次确实非爆了。

但是有趣的是，当我在妮姬社区进行了面向社区的调查问卷时，我发现，调查问卷的反馈与数学计算似乎相差甚远。

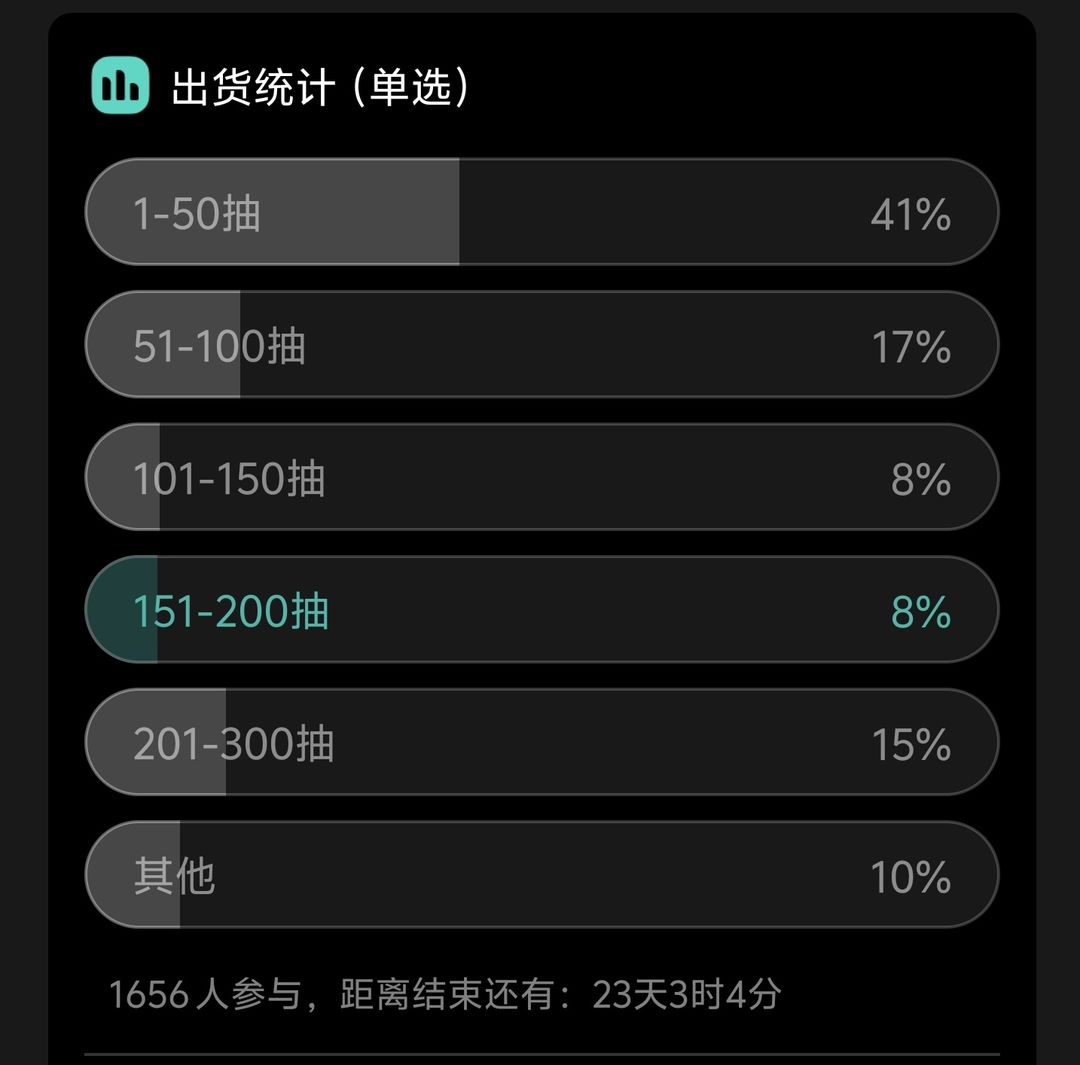
我当时投票点错选项了，实际我应该选201-300

根据社区统计数据，1-50抽的出货人数还可以对的上期望值，但是越到后面越奇怪，尤其是201-300抽出货人数更是违背数学规律。

所以只能说，有保底的抽卡手游才是好抽卡手游，不然有时候不仅不讲道理，还不讲数学。