一些概率计算上的问题(干货满满)
修改于2023/05/14490 浏览综合
本期并未正式计算出结果,只是阐述一下进展以及列出部分过程
但是有了这些之后 结果就已经信手拈来了,只需要我克服自己的拖延症就行了……
正式的计算结果肯定会比较简洁
在上次算完那个问题之后,虽然有很多不确定的地方,不过可以肯定一点,我的结果是不能够表达白嫖罗汉概率的。
目前来说存在的问题还很多:
1.人偶到底能通过什么方式获得,钓鱼还是开宝箱,还是都能
2.如何计算获得18不同人偶的平均次数
3.已证实官方给的概率肯定有问题,不知道正确的概率是多少……
4.人偶到底会不会重复获得
这回主要解决的是算法问题(问题2),其他的还只能按照之前的思路。算法上出现的问题很麻烦,目前有两种思路:一种是按照古典概型算,把每次出新人偶的期望加起来得到抽出18人偶的平均次数;另一种说不能用古典概型算,应该用条件概率,每一次都把出和不出的概率分类讨论,最后再算出他们的平均数。
算法二得到了好多数学上很有成就者的支持,但是没人能准确的直接说出算法一的具体错误,而且算法二的计算量太大了没法算(有整整18!种可能,每一种都要乘18次)。有的大佬给出了简化的方案,不过后来发现有漏算的情况,我也没有找到一个权威的说法到底该怎么简化,我自己推的话……还是算了吧我太菜了
不过想不通不代表做不通,我决定亲自试一试来算出抽出18人偶的平均次数。一开始做了18张卡来回抽,后来发现每次抽都要洗7次牌 太麻烦了(理论上平均洗7次牌才能使牌堆顺序随机),效率极度低下。之后找了个随机程序,随机18个一次一次点,但是发现还是太慢了,点半天才能得出一次成功的次数。然后我就想到,这种大规模的实验,直接编一个程序来模拟不就行了?又快又准确。这样的程序思路很简单,Python的话只需要用到循环结构和判断结构就行了,以正常人的实力完全可以做到。计划可行,开始工作。
下面解释一下一些理论问题,不能保证对 但是我已经尽力了(部分内容取自某百科)
对于电脑伪随机数可靠性的问题,我也做了一些了解。电脑一般情况下是利用一套公式进行复杂的计算,得出的数经过一定的条件判断再输出。电脑通过发送种子数值,运用算法产生某个看起来像随机数的数字,但是实际上这个数字是可以预测的。比如说,如果攻击者掌握了某随机数生成器使用的种子数值和加密算法,如果随机数生成器完全依靠种子数值和加密算法生成密文,这个过程中不添加任何额外随机性,如果攻击者掌握的情报足够多,他们可以逆推来确定加密算法一定会用到的伪随机数,也就能破译密文。所以说,伪随机数不是真正的随机。
真随机数

再进一步讲述之前先解释一下随机事件的概念:在实验发生之前不能确定结果的事件,就叫做随机事件。之所以要解释,是因为大多数人心中的随机事件不是这样的。比如说:
以下是某位同学的观点
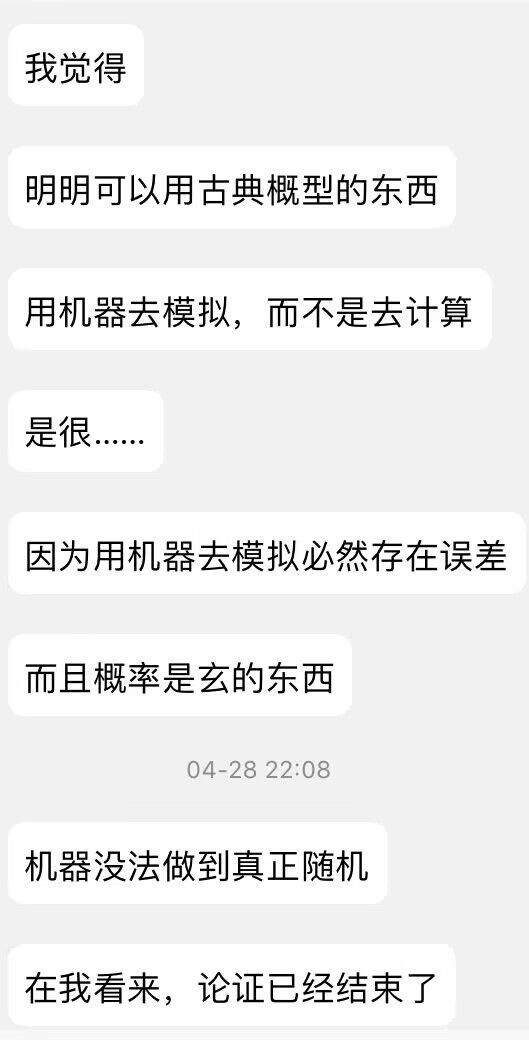
我认为,这能代表大多数人的误区,包括我个人之前的误解。
简单来说,随机事件分为两种(我自己编的,不知道是不是有这个说法)。第一种是一定条件下可以被预测的,包括但不限于:抛硬币,掷骰子,电脑的伪随机数;第二种是不能被准确预测的,包括但不限于:原子中某个电子的具体位置,渣土的崩塌,天气的下一步情况。
第一种其实严格来说不能算是随机事件,但是由于我们日常生活中约定俗成的将它当成随机,所以我也把他放在这里了。
抛硬币的话,如果能够收集到硬币抛出时的受力面积范围大小以及方向等详细数据,是可以计算出结果的,掷骰子也是同理。伪随机数的话,上面解释过了。
第二种其实情况不多见,这几个例子就非常典型。第一个电子的例子因为尺度低于普朗克常数,涉及到量子不确定性,我们说它是处在一个量子叠加态,他的具体地点是不能被准确表示出来的,只能表示他在某个位置的概率。故此他是真正随机的,非常离谱的随机
第2、3个例子,他们的原理是一样的。由于这两个系统过于不稳定,一些极其轻微的干扰都会使结果产生巨大的变化(突然想起来三体运动也是属于这种),所以无法预测。蝴蝶效应正是描述这种不确定性的。还听说过一个例子,某个科学家将天气数据带入一个模型进行预测,然后中午吃饭去了把计算机休眠,回来之后算完发现跟同事的结果天差地别,重复计算发现还是同事的结果。最后才知道,是计算机休眠自动保存,把原来计算中的小数点后20位给保存成了后6位……这种精密的系统,当前技术确实完全无法预测。
那位被我举出来的同志(dbq),他的误区在于,错把随机当成了我说的第二种情况中涉及量子不确定性的部分。而且他也没有理解伪随机数的概念,虽然说伪随机数是可以被预测出来的,但是他实际上是服从理论上随机的数列分布的,所以对于我计算的结果是不会有影响的。
好像扯太远了……
总之,经历了亿点点歧途之后,我确定了设计程序具体思路:建立一个列表,其中元素为0~18的整数,利用随机函数在1~18之间取值,取到的数在列表中删除,直到列表中只剩下元素0为止(这就说明已经把18个数都取一遍了)。这时候记录取值的次数,利用for循环多次实验后把每个单次实验的结果加起来除以总实验次数,就能得到可放回情况下把取18个数都取一遍的平均值了
即:得到18不同人偶的平均次数。
这是我写好的程序
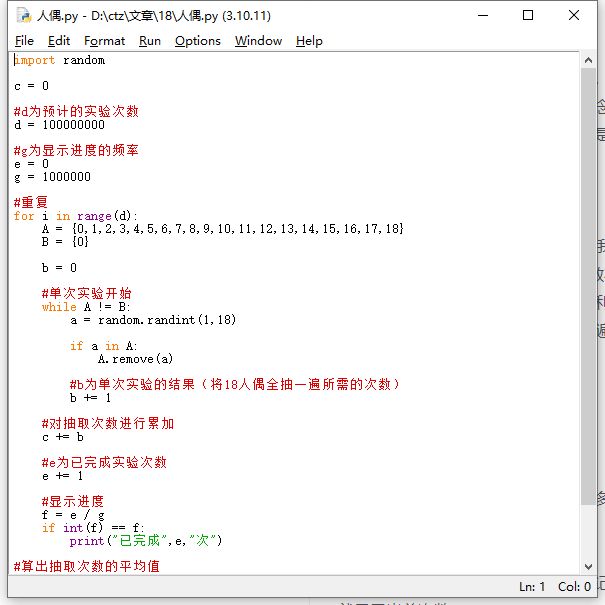
可以看到,涉及到的内容都非常简单
但是没人知道我在这破玩意上面卡了多久!!!
程序每次运行,实验都会进行1亿次
后来我还优化了一下,加了一个进度记录,原理是利用判断当前次数和想要记录的次数相除的结果是否为整数,是就显示当前次数。
听着很简单,但是光这个优化的思路就想了一个星期,试过了好多局限和不可行的方案,最后还是跟前师父的讨论中冒出的灵感……
以下是计算结果
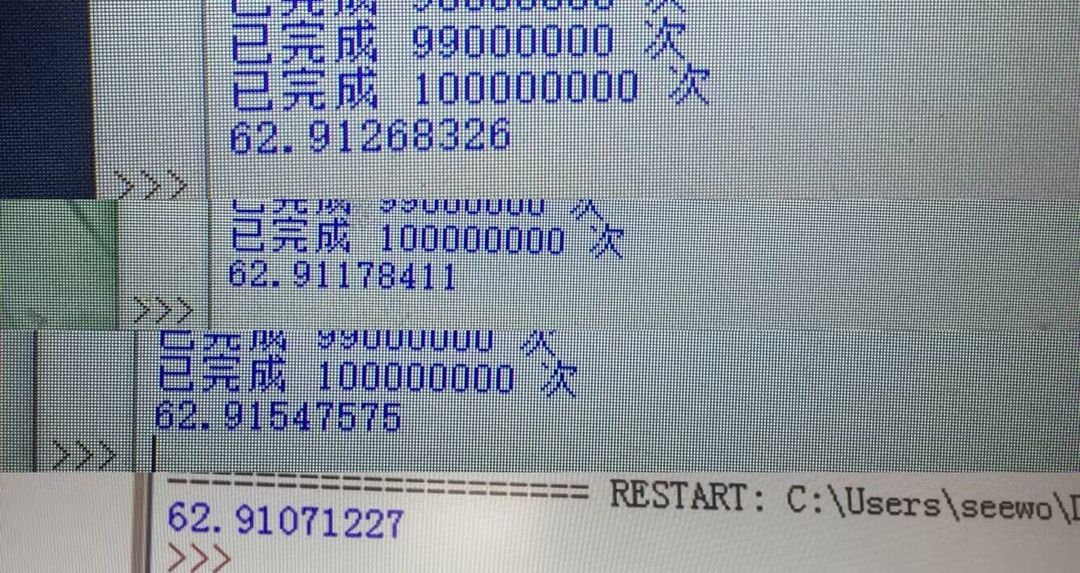
以上只是截下来的几张,实际上还做了大量的重复运算 但是没截
总之,在经历了大量的运算后,可以看出得出的数据趋近于62.91
也就是说,平均需要62.91次才能拿满18人偶
为了和方法一进行对比,我还需要按照方法一计算出来
18个人偶 将每次出新人偶的预期加起来
18/18+18/17+18/16+...+18/2+18/1
=1+18/17+9/8+6/5+9/7+18/13+3/2+18/11+2+9/4+18/7+3+18/5+9/2+6+9+18
=45+18/17+18/11+18/13+27/8+24/5+27/7
通分后相加 得
45+10967079/680680
≈16.11+45
=61.11
可以看出,这和程序模拟出来的结果非常接近,但是还有差别。如果模拟没有出现问题的话,这说明方法一还是漏算了一些情况的
不过在数不大的情况下 利用方法一去估算一些比较复杂事件的预期也是可行的,计算简单而且比较接近
题外话,之前还试着利用AI来进行数学上的计算,但是发现,文字型AI的数学水平完全不值得信任……
同一个问题,他能给我一大堆不同的答案。得出的答案有大有小,大到10³²,小到10……我就不明白了,平均10次能抽出18人偶?只能说6
以上部分的稿是之前写的,但是懒得改了,所以直接贴上了……后来解决了一下前面那几个基础问题
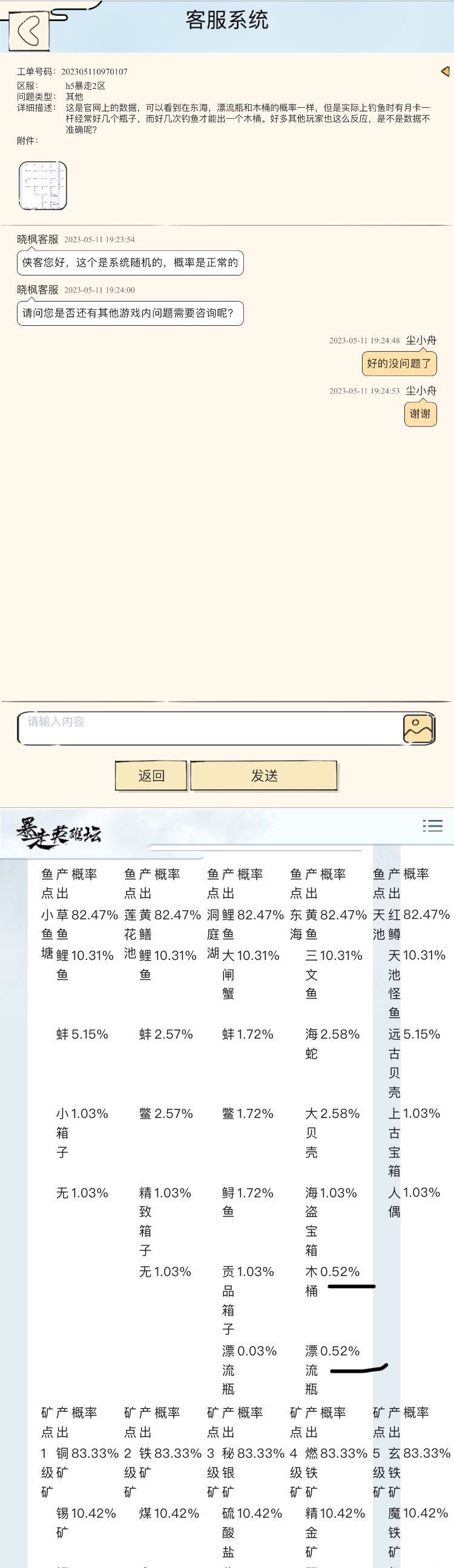
有一天我突然想到,这些问题与其问大佬,倒不如直接问客服呢!
于是我开始跟客服对线

(虽然还有很多不满意的地方,但是真的很感谢这几位客服,耐心的回答了这么钻牛角尖的问题,很抱歉耽误你们时间和精力了)
在长达一整天的对线中,我从惜字如金的客服口中扣出来以下信息:
1.人偶能够重复获得
2.官网上的概率是绝对正确的,你抽不到是你的问题(确信)
3.人偶只能通过在天池钓鱼来获得,其他的
只能是特殊活动了,上古宝箱是不能开出人偶的
4.钓鱼时奖励是按照每个出的东西来算的(每5分钟一次奖励,每次无月卡2样东西,有月卡4样,每个东西计算一次概率。以后简称为每次 每个)
5.具体请玩家自行体验呢~
前三条都能从对话记录中直接找到证据,第四条是我推出来的。我在询问关于每次每个的问题时,客服总是会回答含混不清,或者顾左右而言他。也许相关问题涉及公司算法机密吧,对此我表示 完全可以理解。
我在询问是每次还是每个算奖励时,客服回答是每次,在我清楚讲明每次来算会出现的逻辑问题后 仍然说是每次,并且没有正面回答我的问题。我换了多种问法但是都没能得到准确的答案,所以擅自推导了一下。
我认为是按照每个来算的理由如下:
1.一次奖励可以出多条鱼
2.月卡是奖励次数翻倍,与此同时经过个人观察发现有月卡时奖励的稀有物品(如漂流瓶,宝箱)频率和无月卡时相比也大幅度增加
单看第一条还有疑问,可能是鱼是按照每个算,特殊物品按照每次算,但是联系上第二条就没有问题了。如果特殊物品是按照每次算,那么有月卡时出的频率不应该增加的。所以问题就解决了:钓鱼是按照每个算的。
这样的话,所有的问题就都已经解决了。唯一的问题是还不能在理论上计算出准确的值,不过应该问题不大了。
本篇有点啰嗦,不过没关系,估计还是没有人能看完吧.

